From traffic signals to ambulance and police vehicle sirens, red is an omnipresent color in our world. The wavelength of red makes it the least scattered color for the human eye.
The other day, on the drive back home, I got caught by the red light at a traffic signal. As I waited for those twenty seconds to pass and for the signal color to change from red it hit me… why red? Why not a blue signal? Or just the normal white color of an LED?
From traffic signals to alarm bells, from the red flag of the guards at the train station to the rear lights of a vehicle when its brakes are pushed, red seems to be everywhere—unnoticed, yet very noticeable in significant times. What makes the universal choice for the sirens of police vans, ambulances, and so many other warning signals?
Even though many associate this color with their romantic pursuits, displaying it through roses and heart-shaped stickers, red has a far greater significance in our daily lives; it is, after all, the color of the fluid running through our arteries and veins (even though a slightly different shade of red).
Recommended Video for you:
What Makes Red So Special?
As always, science will help us figure it out!
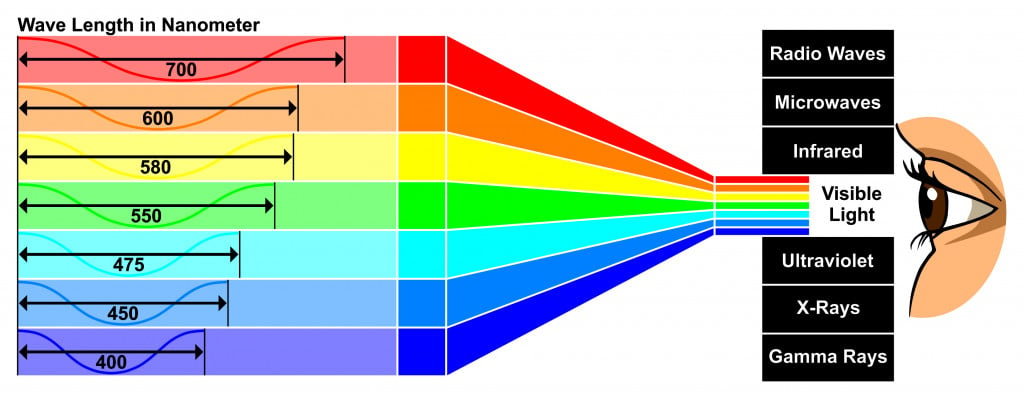
We first need to understand that the color red is a component of the visible spectrum of light—VIBGYOR—formed due to splitting of the white-colored light waves.
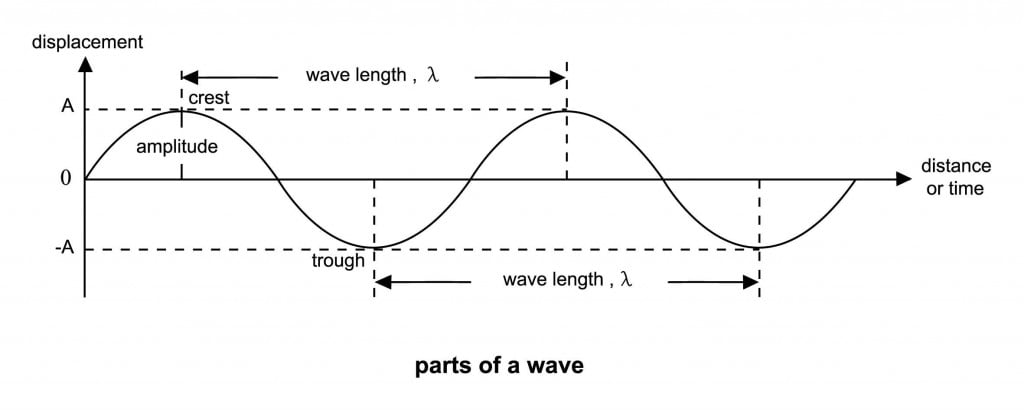
Now, these light waves have a property called wavelength. According to the wave theory of light, the wavelength (lambda: λ) of any wave is the distance between two successive crests (the upper peaked portion) or between two successive troughs (the lower peaked portion). Wavelength is calculated by multiplying the velocity of the wave with its frequency. We all know that the speed of the light is the easy to remember figure of 3×108m/s.
Frequency can be a bit trickier to grasp. Frequency is the reciprocal of the time that the wave takes to travel the distance of one whole wavelength.
What Is Scattering?
The answer to why red is effective as a danger signal lies in a concept called scattering. Scattering is the phenomenon in which light get deviated from its straight path upon striking a hurdle, such as dust, gas molecules or water vapor. The beam of light is redirected in different directions after interacting with the particles present in the medium.
There is a law that governs this phenomenon of scattering called Rayleigh’s scattering. This law states that the scattering of the light is inversely proportional to the fourth power of the wavelength of light.
The scattering intensity is proportional to λ−4
Do We Want Our Danger Signals To Scatter?
Think about it… do we want our danger signal or alarms to be visible from far away? Yes.
All the important signals that must catch one’s attention, such as danger or alarm signals, must use a color that is visible from a distance so that people can be notified and mishaps can be prevented. Therefore, we need light that does not scatter much and is in the visible range of humans; how else would we be able to ‘see’ it?
From the electromagnetic spectrum, the range that is visible to humans is called the “visible range” of light. This range extends from the blue color (having the lowest wavelength) to the red color (having the highest wavelength). The wavelength of red light is about 620-750 nm. The Scattering Law states that the longest wavelength will scatter the least. Red satisfies both of these conditions: first, it belongs to the visible range of humans, and second, it has the highest wavelength, making it the least scattered color.

Our distress or alarm signals should remain visible, even when the visibility of the surroundings is low. The immediate visibility can be affected in circumstances, such as fog, rain, and smoke. Since we want the signal to reach a greater distance, it must scatter less. For it to scatter less and pass easily through fog, smoke, etc., the wavelength must be high. That is precisely why red comes to the “rescue”…both literary and figuratively!
The Effect Of Red On The Human Brain

An interesting study published in the journal Frontiers in Human Neuroscience linked the color red to attracting attention in an emotional context.
Motor responses are the responses shown by the human mind and body in response to any kind of stimulation. It was established in the study that viewing the color red immediately before or during a motor response increases the response’s strength and velocity. However, another study found that viewing the color red before a motor task actually inhibits motor responses, and the researchers suggest that this happens due to the elicitation of fear.
Moreover, the red color seems to possess emotion-eliciting properties. It was shown that people tend to associate red with negative, danger-bearing emotions, since it is the color of fire, blood, anger, and sometimes of poisonous or dangerous animals. (Source)
Therefore, the human mind is immediately activated or alerted when it sees this color. It is established that signaling is one of the most important functions of a color. The color red should therefore be able to catch our attention, particularly in emotional conditions. Based on the research above, it seems like red plays its role pretty well in the human brain.
Effect Of Red In The Wild

To delve into the effects of this color in the natural world, we find that it is equally prominent there for signaling. It is easily visible both against the blue background of the sky, and on the green of foliage. Prey can identify a red-colored predator flying towards it. On similar lines, it is easy to spot a red-hued prey moving or slithering near the green-colored leaves. Also, we can thank bird pollination for most of the red flowers that we prize in cultivation. The color red often attracts birds. On the other hand, white, yellow and blue colors attract insects. Seems like the natural world has already studied physics…

To conclude, even though we tend to overlook the importance of the color red in normal circumstances, it is rarely overlooked in situations of grave importance or those demanding immediate consideration. So, the next time you stop at a traffic signal, pay attention to how you reacted to the color red without really noticing it!
References (click to expand)
- 7. Rayleigh scattering. Princeton University
- Wavelength of Blue and Red Light. The University Corporation for Atmospheric Research
- Piazza, R., & Degiorgio, V. (2005). Scattering, Rayleigh. Encyclopedia of Condensed Matter Physics. Elsevier.
- Kuniecki, M., Pilarczyk, J., & Wichary, S. (2015, April 29). The color red attracts attention in an emotional context. An ERP study. Frontiers in Human Neuroscience. Frontiers Media SA.












