Table of Contents (click to expand)
The Infinite Chocolate Paradox is a phenomenon where a chocolate bar can be cut into pieces and rearranged to create an extra block of chocolate. This is possible because the chocolate bar is made up of infinite chocolate blocks, which can be rearranged to create the extra block.
In Jan 2018, a chain of French supermarkets decided to sell Nutella, also known as God’s sacred nectar sent from heaven, at a 70% discount. This astonishing slash in price resulted in what one could logically expect – a riot.
However, I’m not using the word ‘riot’ in its metaphorical sense. I mean it in the literal sense.
The ‘riots’ spread across the supermarkets forced them to summon the police for help when customers resorted to fighting and jostling. While the hunt for discounted chocolate saw one woman’s hair being gruesomely pulled, another one’s hand was profusely bleeding.

We love chocolate. We love it in all shapes, sizes, colors, flavors, and packaging. Jerry Seinfeld joked that the only goal of his entire childhood was to buy candy. His happiness knew no bounds when he first became familiar with the concept of Halloween, to which he remarked in disbelief — “Everyone we know is just giving out candy?” He promises he will “do anything they want,” and after a short pause – “Yes, I can wear that,” he concurs.
If there’s something repulsive about chocolate, it’s that it eventually finishes.
But what if there were a way to produce endless blocks of your favorite Hershey’s bar by simply breaking it up and rearranging the pieces? Don’t believe me?
See for yourself.

Recommended Video for you:
What Is The Infinite Chocolate Paradox?
This phenomenon, known as the Infinite Chocolate Paradox, spread like a plague and caused outrage on social media. The procedure is simple: Take a chocolate bar that consists of 5×5 chocolate blocks. Cut the bar diagonally from slightly below the second block (from below) on the left of the vertical sides to slightly above the third block on the right.
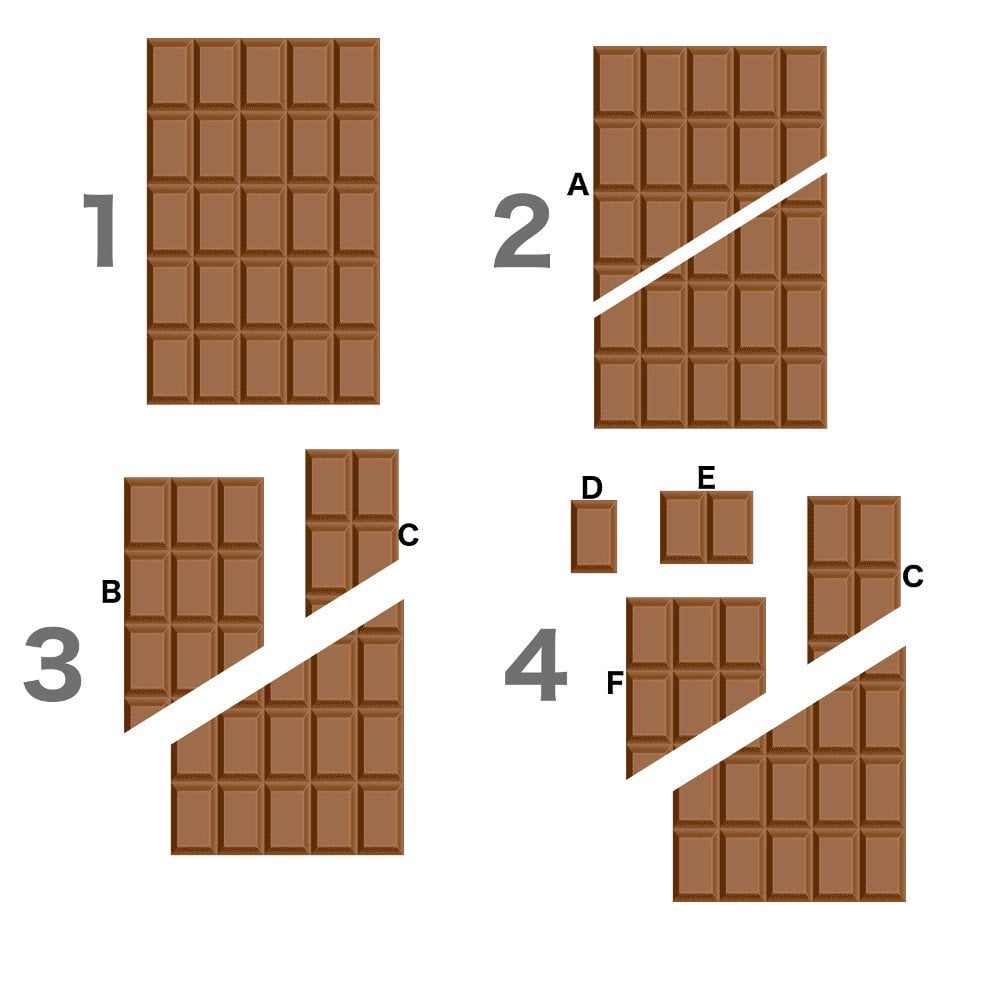
Next, slice the newly amputated piece, which we’ll call piece A, vertically from the third block (from the left) on its upper end. Let’s call this piece B and what remains as C. Chop off a square (D) and a 1×2 rectangle (E) from the chocolate blocks constituting the first three blocks of piece B. The remaining piece from this partition is F.
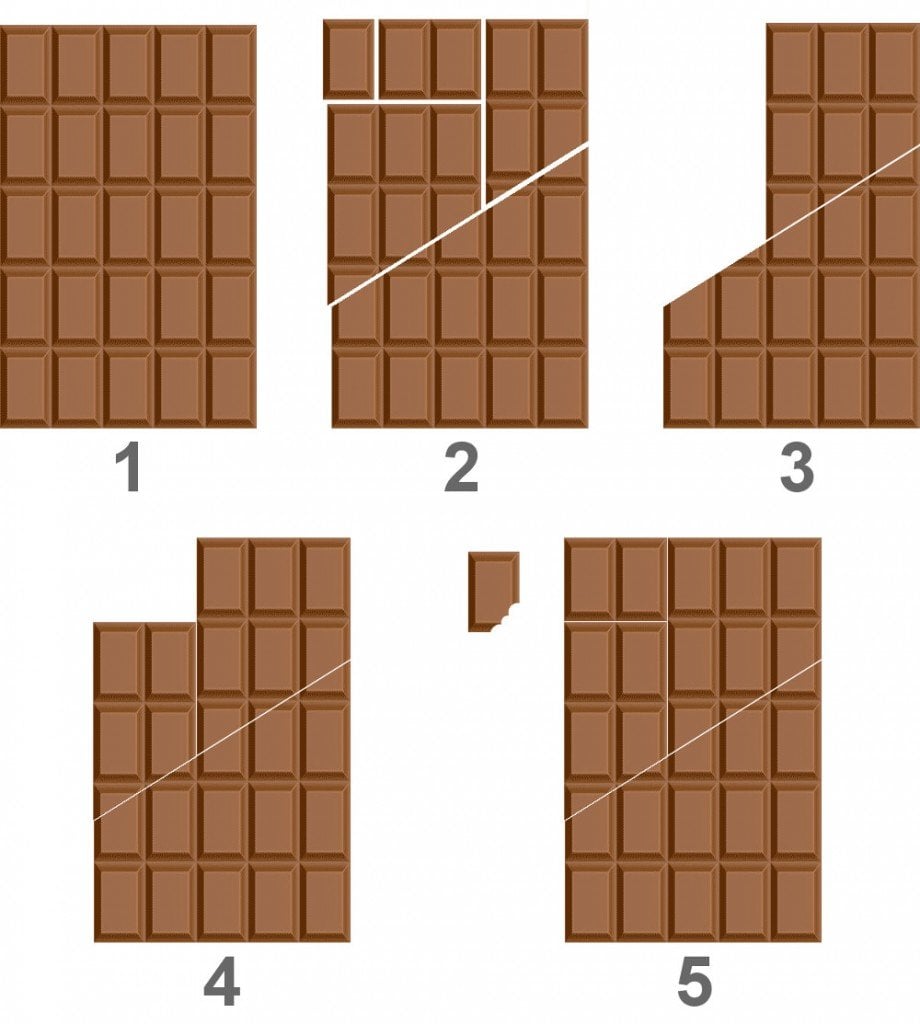
Now, let the magic begin. Shift F to the right and fill the void left by F by placing C in it. Next, play the easiest game of Tetris by dropping the 1×2 rectangle over the 1×2 void above C. The 5×5 block is rearranged, with an additional block of chocolate to spare. Repeat this process to obtain infinite chocolate!
The Banach-Tarski Paradox
Of course, this isn’t plausible (duh). The gif illustrating the paradox is grossly skewed; it is only an illusion. Calling it an illusion implies that it is fake, which is because when the pieces are rearranged, the resulting bar isn’t the same bar we began with. Measure the vertical lengths of the two bars before and after performing the procedure, and you will realize that this absurd way of cutting it in half has rendered it slightly shorter. The apparently extra block of chocolate comes at the cost of reduced size.
The infinite chocolate paradox is a crude representation of the Banach-Tarski paradox, which, through a notorious misinterpretation, allows the most daunting mathematical atrocity — 1=2. According to it, it is possible to divide a solid 3D sphere into 5 pieces and rearrange them to form two identical copies of the original sphere! There isn’t even stretching involved, only reassembling will produce replicas of the same density, same volume, same everything.

The mathematics underlying the paradox is, as you may have guessed, extremely esoteric and therefore incomprehensible, defying common sense and challenging our intuitive perception of spatial concepts such as “volume” and “density.” It operates in the strange realm of infinity, a concept that has always puzzled mathematicians.
The ridiculous phenomenon is possible only if one assumes that the sphere or matter is generally infinitely divisible, which it obviously is not. The matter is based on rigid structures held by atoms. The concept is applicable only in the abstract world, not in the real world, because, in the real world, the matter is limited by size.
However, in the abstract world, where the paradox is possible, matter can simply be considered a collection of points, in this case, infinite points.
Different Infinities
The paradox deals with measurable sets composed of immeasurable quantities. Consider the set of numbers 0,1 and all the numbers between them. This set is denoted by [0,1]. This measurable set can be further divided into uncountable, infinite real numbers starting from 0.000000000000000000001 followed by 0.0…2 and so on.

The length of these infinite numbers can be divided into two halves. The points constituting both the halves have the same cardinality because infinity divided by two is still infinity. This implies that there are as many even numbers as there are natural numbers!
Another way to magically conjure an additional set of infinite numbers from a given set of infinite numbers out of thin air is to distinguish between ‘countable’ and ‘uncountable’ infinities.
People who believe that the number of natural numbers until infinity and the infinite number of real numbers between them are equal, such that each natural number can be assigned to each real number, are clearly wrong. This is because you can diagonally move down the real numbers and simply increment the numbers you progressively parse.
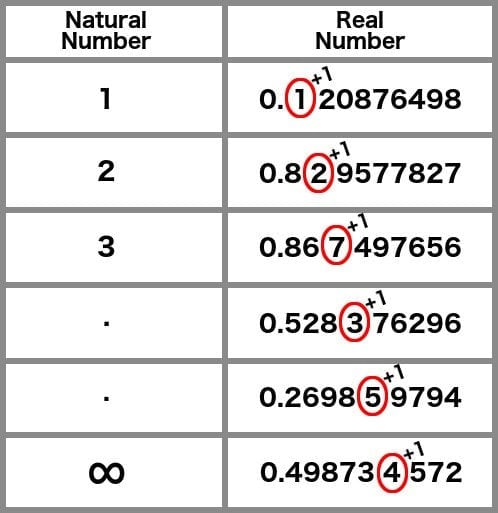
Since all-natural numbers are exhausted, as they are ‘countable,’ there are no new natural numbers that can be assigned, meaning that the infinity of real numbers is greater, up to ‘countable’ than the infinity of natural numbers. We can now separate the newly created numbers to form another set of infinite numbers.
This explains how the sphere can decay into two identical spheres, albeit by painful simplification, as the density reduced to half is still infinite.
Remember that this only works for mathematical points, not for physical atoms.
Moreover, the five shapes into which the sphere divides are highly eccentric, complex, and distorted entities, unlike any “shape” you have ever encountered.
Enjoy your finite bar of chocolate.













