Can Economics (Game Theory) Help You Win A Game Of Chess?

Game Theory can be used to win chess using Zermelo’s, Nash Equilibrium and Prisoner’s Dilemma strategies to make a chess Game Tree.

For half a millennia, chess has been a favorite pastime (or obsession) among war strategists, geniuses and anyone who values the art of competition. Today, we might play chess for self-interest and tactical development, but 1300 years ago, it was invented after being inspired by war strategies, with pieces that inspired modern-day chess. Horses, elephants, and counsellors of ‘vizir’ continue to be important chess pieces in various countries and regions.

We have played, critically assessed and reformed the game for over 1300 years. A 32-piece modern-day chess game is far more complicated than the 7th Century Chaturanga, meaning “four limbs” in Sanskrit or Chatrang in Persian. However, its characteristics as a “game” has not changed. To win, we still need impeccable tactical game knowledge. Simply put, you need to know the game theory.

Recommended Video for you:

What Is Game Theory?

Mathematically, games are a competition of pure strategy between ‘n’ number of players to follow the rules for a pay-off (a reward). Game theory analyzes such games to predict or calculate winning moves. 

Imagine it as an issue of probability, but better. 

Although the name came later, game theory dates back to 500 AD. It was also heavily implemented in:

• Two-person game-of-chance strategies 
• Theory of Wealth in the Economy
• Charles Darwin’s theory of Natural Selection
• Determining trade outcomes in Duopoly
• Zermelo’s history of the Game Theory (using chess)
• Prisoner’s dilemma
• Poker, business and war strategy
• Battle planning of World War 2
• The Logic of animal conflict

… in that chronological order!

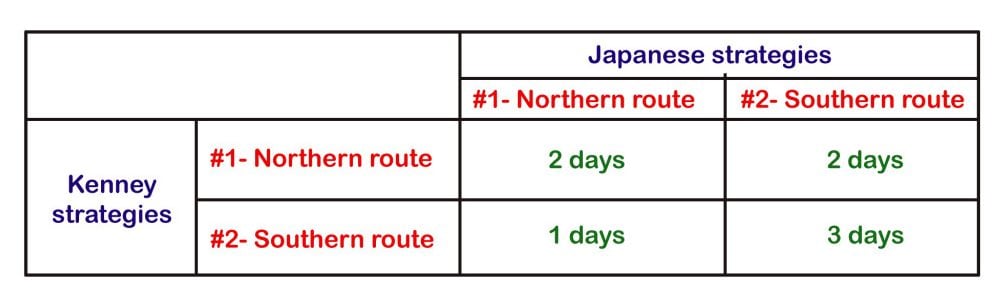
Here, we have an old war-time example of Game Theory and how we can build a strategy using it. During the Battle of the Bismarck Sea, the American General predicted that the Japanese Navy would either take the Northern or Southern route around New Britain.

Using different routes would result in different attack timings for both.

The North route would take 2 days of bombing, due to poor visibility costing an extra day, while the South route would allow for 3 days of bombing. In the game matrix, using the Northern route was safer for both. This mathematical prediction shows how using the Northern route would mean a better possibility for an attack on both sides, i.e, saving the Japanese from 3 days of continued bombing and 2 days of bombing on the part of Kenney (since the Southern route promises only 1 day of bombing Japan). It saves Japan from a worse-off scenario and gives Kenney maximum days available to destroy Japanese forces. History shows that’s exactly how the war went down!

Such zero-sum games are useful for predicting moves, in both war and chess.

Surprisingly, the first ‘Theorem’ of games was made by Zermelo to mathematically analyze how either of the players can win in a given round of chess.

Zero-sum Games

Chess begins with 32 pieces on a 64-square board. The queen is the most powerful, each player has a king & a queen, 8 pawns, 2 bishops, 2 castles, and 2 knights. The objective is to eliminate the king by rationalizing and executing strategies. 

Now, what does it mean to behave rationally? Intelligent thought in people is known as rationality. In 1928, Von Neuman Morgenstern launched the study of zero-sum games, stating how chess is the perfect example of rational behavior. A player can force an outcome (them winning), which would be the best possible outcome of the game, provided they play rationally. 

In chess, each rational player has an opposite interest, i.e, the zero-sum game. One player tries to maximize their chances of winning using a strategy, while the other player’s strategy changes simultaneously to minimize their chances of winning. There are also simultaneous games, wherein players know the possible outcomes and their opponent’s moves before making their own moves.

How can they make the right decisions that will guarantee a win? We can use either Nash Equilibrium or Prisoner’s Dilemma.

Nash Equilibrium

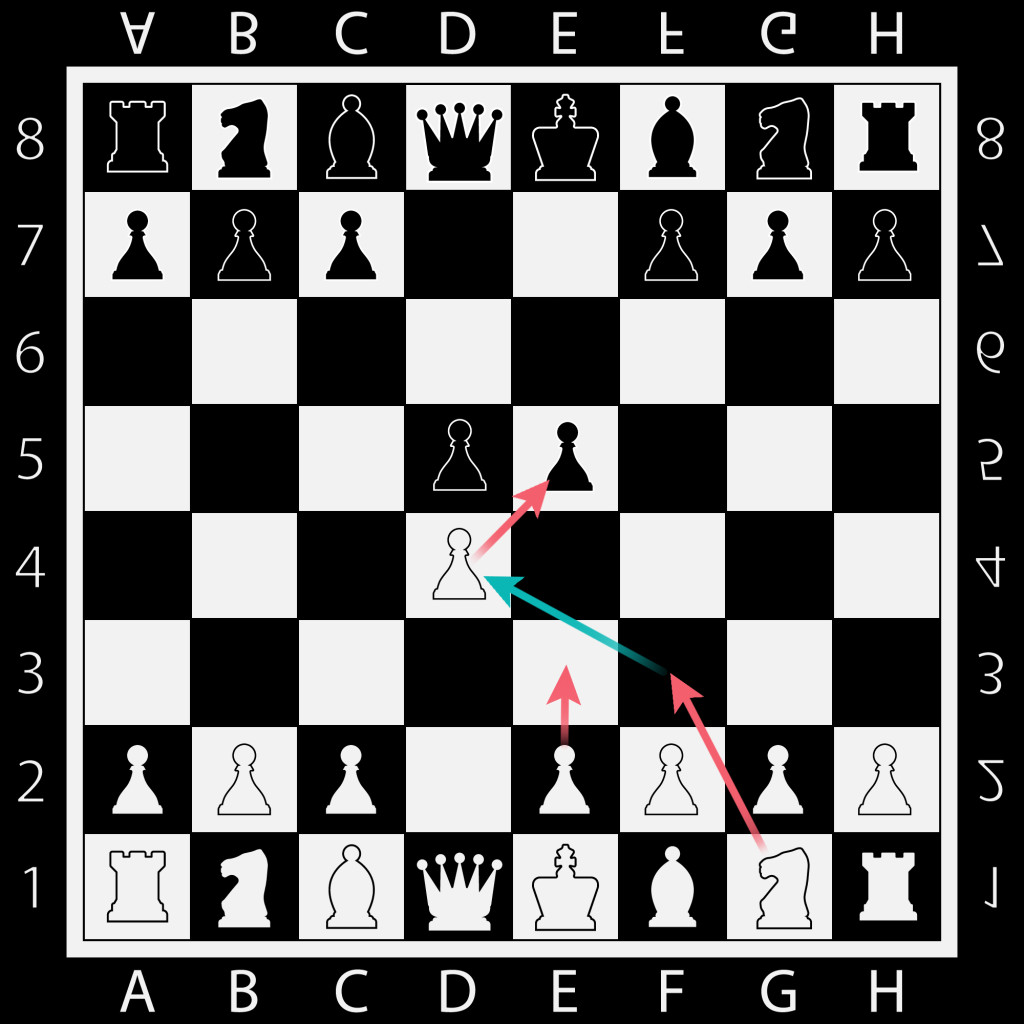
Let’s assume black as player 1 and white as player 2.

Given a select number of decisions of player 1, they know the number of possible moves that player 2 can make. Player 1 will either have a better pay-off with the predicted move of 2 (e.g., take over the opponent queen) or have a less worse pay-off (sacrifice a bishop to save the king). We can build a Game Tree with such sequential moves by calculating multiple equilibria.

Prisoner’s Dilemma

The original layout of the Prisoner’s dilemma is between two people who might go to jail for a crime. Here, if both refuse to confess and remain silent, they are imprisoned for a year (A:-1, B:-1).

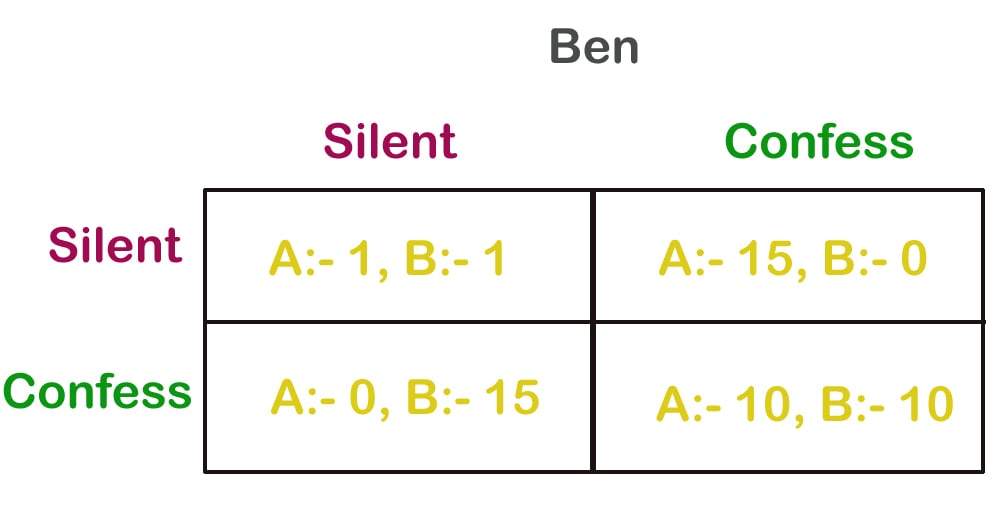
If only Ben or only Alan confesses and blames the other, either one of them gets 15 years, depending on who confessed first. Whoever confesses first gets a lesser sentence when both Ben and Alan choose to confess. If both confess simultaneously, they get 10 years each. Their pay-offs depend on the opposite person’s decision.

Similarly, in chess, we can build a similar table to calculate winning moves, given the opponent’s predicted move.

Zermelo’s Theorem: Answering The 2 Questions In Chess

Now you know the process to strategize a game of chess, but the most important questions remain unanswered:

Can we predict a player’s winning position? Or, when can it happen in the game, mathematically speaking?

We need a non-empty set of all moves required to win a game for white, not considering black’s moves, in sequential order. If it is an empty set, there is a draw. White can also have another set containing moves that can postpone their chances of losing. However, according to the rules, a game cannot last forever. They must reach a point where the position of the pieces is repeated thrice, causing a draw. Now we consider this set to be empty too. This implies White must make a finite number of moves to postpone their losing probability. When this happens, Black can use the opportunity to win.

So, either of the players can force their win with a strategy if they know the finite number of moves their opponent has to postpone losing.

When they reach this winning position, how many moves would it take for them to win?

According to Zermelo, it takes as many moves as the number of positions in the game to win, or even fewer, at times, but never more. Let’s prove this by contradiction.

If Black can win with more moves than there are positions on the board, then their winning move must have been repeated at least once. However, if they have repeated the position before, they should have won then. This proves that if Black uses the winning move, they must win the game, causing no repetition and a thus lesser or equal number of moves as the positions.

As for you, there’s no need for contradiction. Try building a Game Tree using Nash Equilibrium to build a personalized (and unbeatable) strategy to win in all the chess games you play in the future!