Table of Contents (click to expand)
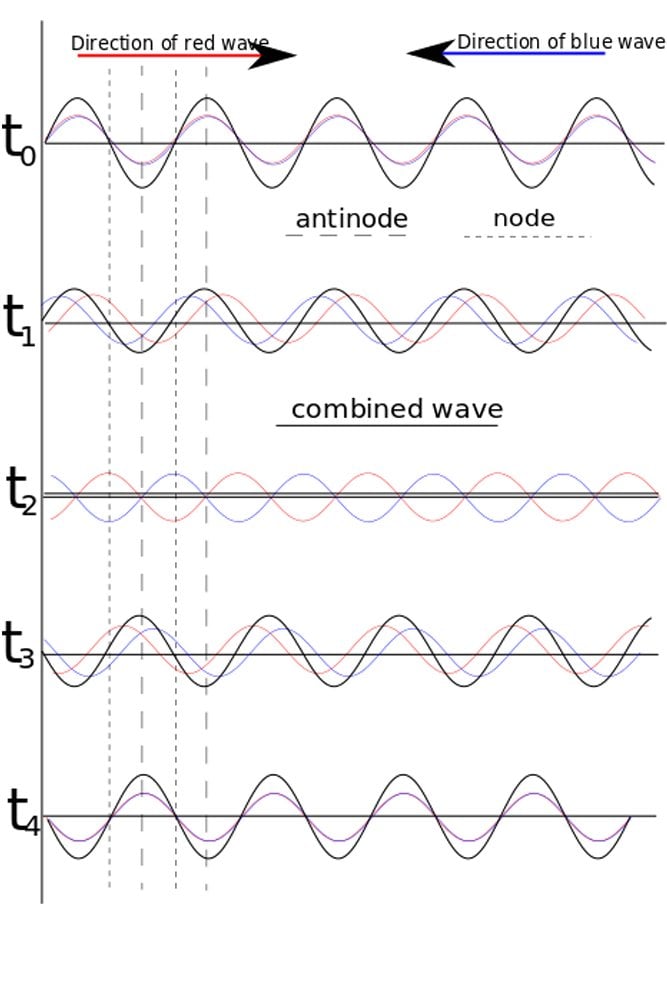
A standing wave is one that is formed by the combination of two waves moving in opposite directions, but having equal frequency and amplitude. A standing wave can only be formed when a wave’s motion is restricted within a given, finite space. In more specific terms, a standing wave is a wave that oscillates in time, but its peak amplitude profile does not move in space.
Also known as a stationary wave, a standing wave is formed due to interference. You see, when waves are superimposed, their energies are either canceled out or added together. In the case of waves that travel in the same direction, interference results in a traveling wave (the opposite of a standing wave).
Recommended Video for you:
How Is A Standing Wave Produced?
Suppose you pluck a string on a guitar. The moment you do that, you create vibrations within the body of the guitar, which are more specifically called mechanical waves. Such a vibrating instrument produces sound because the energy produced by these vibrations (in the form of sound waves) moves through the air and reaches our ears. The vibrations created within the instrument itself (the guitar, in this case) are called standing waves.
Standing waves can only be created when their motion is restricted to a given, finite region. Let’s consider the vibrating guitar string again.
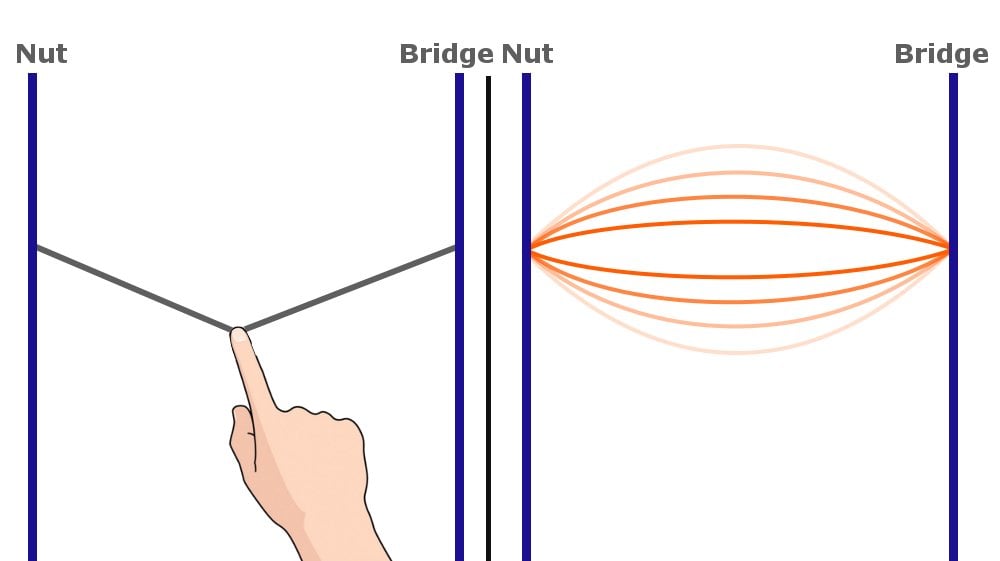
Caption: Notice how a string vibrates when it’s plucked.
You know that the guitar string (that you plucked) is restricted on both ends – by the bridge on one side and by your finger on the fretboard on the other. The moment you pluck a string, the wave reflects off each of the aforementioned boundaries of the string. The energy of the wave spreads out as it keeps moving back and forth between the two ends. Due to the process of interference, standing waves are produced.
Nodes And Antinodes Of A Standing Wave
A standing wave is called as such because, unlike ‘regular’ waves, it does not look like it’s traveling from one side to the other. Rather, it looks as if it were waving while standing in place.
Every standing wave pattern has certain points along the medium that appear to be standing still. These points are called nodes, or ‘points of no displacement’. There are also certain points along the medium that undergo maximum displacement during each vibrational cycle of the standing wave. These points are called antinodes.
Take a look at the following gif to get a better grasp of nodes and antinodes.
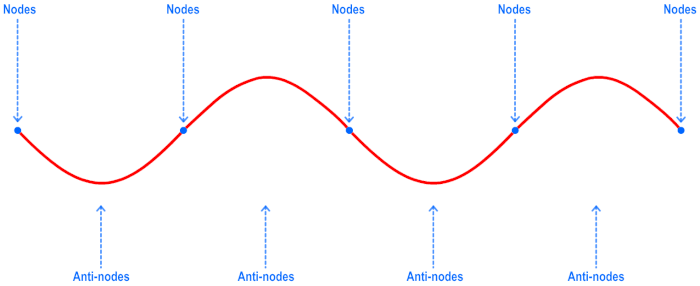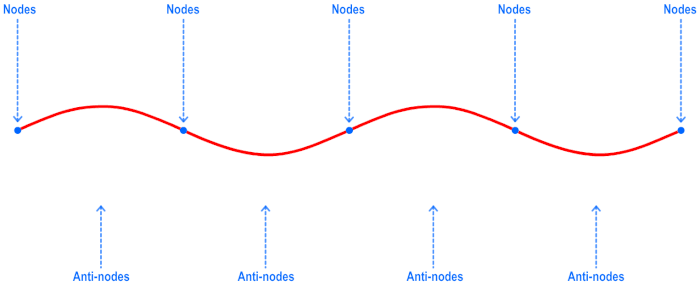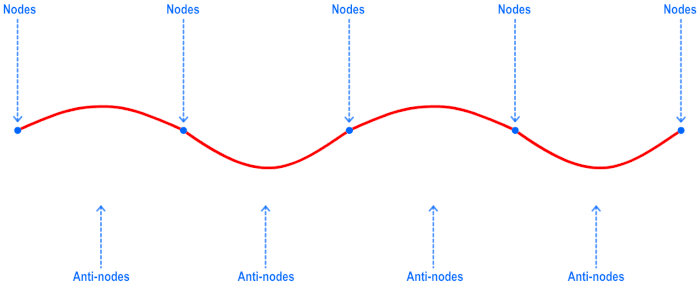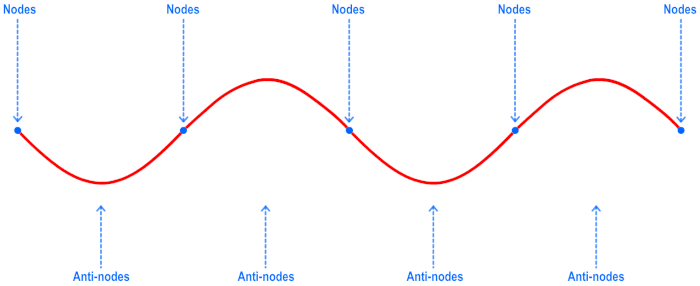
You can see in the gif above that there are some points in the wave that are not moving at all (nodes) and then there are points halfway between two adjacent nodes where the motion of the string has the greatest deviation (antinodes).
What Is The Standing Wave Ratio?
Standing wave ratio (SWR) is the ratio of the amplitude at the antinode (maximum) of the standing wave to the amplitude at the node (minimum).
When you look at a wave with a finite and non-zero SWR, you can assume that the wave is partially traveling and partially stationary. Pure standing waves have an infinite SWR. An interesting thing to note about pure standing waves is that they don’t transfer any energy from the source to the destination! However, the wave still remains subject to losses in the medium.

The term standing wave ratio is of the utmost importance in the field of telecommunications and radio engineering, as it helps in installing and tuning transmission antennas. That’s why checking the SWR (using a device known as the SWR meter) is a standard procedure at any radio station.
Standing Wave Examples
The aforementioned example of plucking the string of a guitar is a good example of standing waves beings produced. Other than that, two people shaking either end of a jump rope is also a good visual to understand the idea of standing waves. If they shake the rope in sync, it can form a pattern of waves oscillating up and down, with points along the rope where the rope’s arc is at a maximum (antinode) and points where the rope is almost still (node).

Standing waves can also be observed in sound waves. The presence of standing waves is most noticeable in musical instruments like flutes or guitars. Standing waves can also be observed in optical media, such as optical cavities, waveguides etc. Even the interference between X-rays can form an X-ray standing wave field!