Table of Contents (click to expand)
Calculus is the study of change, in a mathematical sense. It’s used to find things like the rate of change of velocity of an object (i.e. acceleration), or the rate of change of a function. In short, it allows us to study how things change over time.
Most people dread the world ‘calculus’, and with good reason… it’s the stuff of high school nightmares! It’s a subject that has kept people up at night for centuries with its confusing methods for arriving at solutions. However, I am here to tell you otherwise. Calculus can actually be fun to understand and cherish if we are introduced to its basics in a new light. Let’s start this train of understanding with the fun historical background of this complex subject.
Recommended Video for you:
History Of Calculus
Calculus was invented by two legends of the scientific community: Sir Isaac Newton and Gottfried Wilhelm Leibniz.
Sir Isaac Newton is known as the father of classical mechanics and one of the greatest physicists of all time. He is credited famously for both the laws of motion and the law of gravity, but Newton’s greatest mathematical invention happened to be calculus. Newton enrolled in Trinity College of London, Cambridge in 1661. However, in 1667, the college was forced to close down due to precautions taken for the bubonic plague. During this time, the 22-year-old Newton was trying to solve physics problems, but he needed to invent a dynamic method of mathematics that could explain his theories on gravity, the laws of motions and why planets travelled in ellipses.
He wanted to explain the velocity of an object at any given instant and the reason that planets revolved in ellipses. It was easy to work on problems that had a very linear graph plot, but problems arose when the line or curve was constantly changing. To overcome this, Newton invented an equation that would provide the slope of any given point on any curve at any instant on the curve.
The above equation is what led to the birth of Differential Calculus.
Gottfried Wilhelm Leibniz was born in Germany in 1646 and was extremely gifted as a child, but oddly enough, his first interests were philosophy and theology. He was 18 when he graduated with a Master’s degree in philosophy. Within a year of legal studies, he was awarded a Bachelor of Law. It was a friend of his who urged him to consider taking up mathematics after earning his law degree. In 1674, Leibniz started working on calculus. His approach was that the integral was the sum of the ordinates (Y-axis) for infinitesimal intervals in the abscissa (X-axis).
The above equation led to the formal birth of Integral Calculus.
However, it remains clear as to who can be regarded as the “Father of Calculus”. Although it was Newton who conceptualized calculus in its modern form, it was Leibniz who published the first paper on calculus. Today, it’s widely accepted that both were independent discoverers of calculus.
What Is Differential And Integral Calculus? How Are They Connected?
Before we get into the differences between differential and integral calculus, we must first understand what a function is. A Function is a special relationship where any input has a unique output.
For example, let’s take the function f(x) = x+1. Now, if we take three unique values for “x”, say -1, 0 and 5, we get the unique outputs of 0, 1 and 6, respectively.
Differential Calculus is the subfield of calculus concerned with the rate of change of quantities. The primary use of differential calculus is to find the derivative of a function. The derivative of a function gives the rate of change of a function for a certain input. Let’s consider an example to understand this a bit better. The process of finding a derivative is known as differentiation.
Let’s take a function named f(x). Now, let’s assume that f(x) is equal to x2. The graph for x2 is shown below.
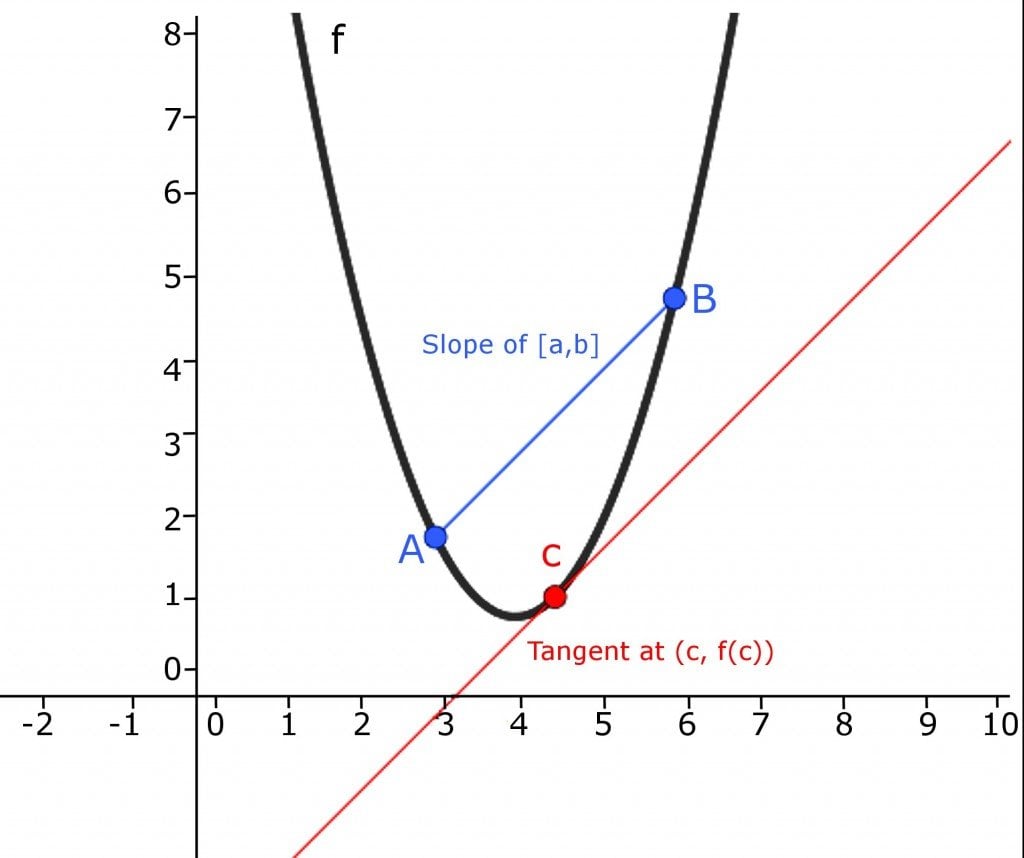Clearly, from the above graph, we’re able to see the geometric representation of a derivative. From the image, we can gauge that the derivative of a point is a slope or a tangent at that point, provided the derivative exists and is defined at that point.
Integral Calculus deals with the mathematical concepts of Integrals. An integral is a mathematical object that can be interpreted as the area under a curve. The Riemann Integral is the simplest and most basic integral.
There are two kinds of integrals, one being the definite integral and the other being the indefinite integral. The definite integral is an integral that has upper and lower limits; in the end, it gives a number –a definite answer – as a solution. The indefinite integral does not have any limits and always gives an answer in terms of a variable. Indefinite integrals are also called Antiderivatives.
The beauty of calculus lies in the fact that there is a link between differential calculus and integral calculus known as the Fundamental Theorem of Calculus.
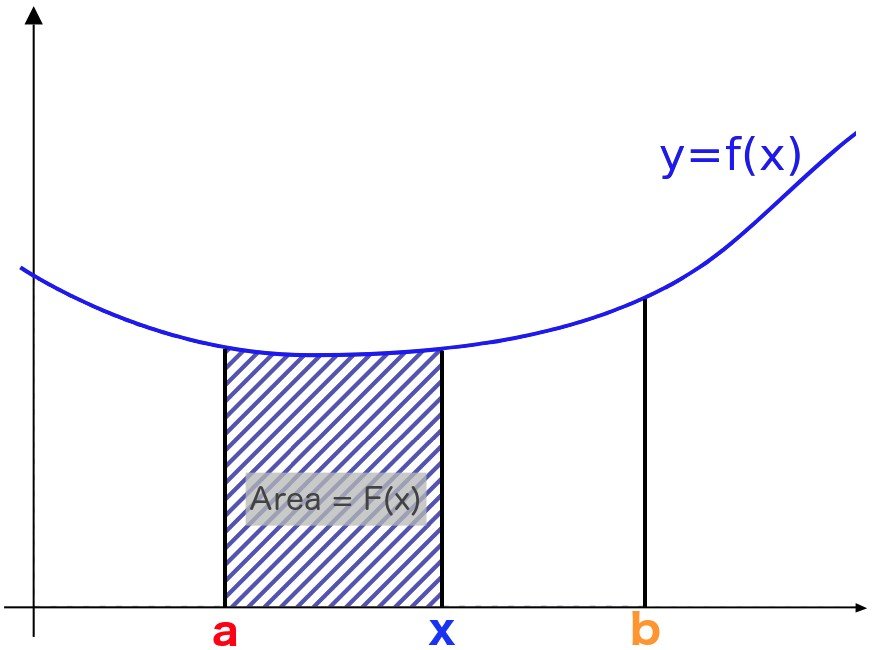
To understand this fundamental link, let us take a geometric approach. Now, as clearly shown in the diagram, a particular area under the curve that is segmented lies between a and b. The area between a and b would be denoted by the Riemann Formula.
Now, if we were to take any point x between a and b, then the resulting area under the curve would be:
Now let this area between x and a be denoted by F(x), where x is the interval [a, b]. The below equation is also known as the First form of the Fundamental Theorem of Calculus.
The Fundamental Theorem of Calculus tells us that if we take the derivative of F(x) on the left-hand side, then the right side is equal to f(x) for any continuous function. The below equation is known as the Second form of the Fundamental Theorem of Calculus.
The Fundamental Theorem of Calculus shows us that Integration and Differentiation are intimately linked to one another. In fact, they are considered inverse operations to one another!
Applications Of Calculus
The beauty of calculus is not only contained within mathematics; calculus is also used to describe the dynamic nature of our world. Calculus is the language of motion and change. If a quantity or system is changing, we can use the mathematical modeling of Calculus to help us analyze, optimize and predict different parameters of the system. Now, let’s take a look at two diverse fields where calculus is constantly implemented.
In Aerospace, a key engineering field, mathematics plays a paramount role. One of the areas where it is used is in modeling the motion of a rocket. The thrust of a rocket into space is the calculus of motion, which is termed momentum, where m is mass and v is the velocity of the object.
The second and third laws of motion framed by Newton are applied. Most rockets work on the principle of variable mass, which might make you wonder how the mass of a rocket is variable?
A rocket’s mass decreases in time as the fuel burns off. As the rocket ignites, it experiences a very large acceleration towards the ground, which propels the rocket forward according to the third law of motion. The force that pushes the rocket upwards is called thrust. Thrust can be defined as the rate of change of momentum. It is also the first derivative of momentum.
After launching, to escape the gravitational forces of the earth, the mass of the rocket must become as small as possible, so the rocket sheds its different parts in different stages.
Calculus is also extremely helpful in Medicine. Doctors use calculus to help determine the rate of growth of tumors. This can be done by the following procedure. Imagine that a patient has a tumor of a small size, and a doctor wants to know the rate of progression or degeneration of a tumor. The mathematical model used for modeling the growth of a tumor can be an exponential function with respect to time.
Vt =V0 * eat
Here Vt is the Volume of a tumor after a certain amount of time. V0 is the initial volume of a tumor, and the term a is a constant with t being the time period. Calculus can be used by differencing the above equation and obtaining the first derivative. This helps the doctor in predicting the tumor growth trajectory in the future.
We can clearly see that Calculus is critically applicable in fields like Medicine and Engineering. However, its application stretches to other diverse fields such as microeconomics, astrophysics, the stock market and radioactive decay. Anything that involves studying the rate of change and finding an optimal solution is an area where Calculus can be extremely useful!
