Syllogism: Definition, Explanation, Laws, And Examples

Table of Contents (click to expand)

Logical Arguments And Deductive Reasoning
Syllogism And Its Structure
Various Types Of Syllogisms
Conclusion

Syllogisms are logical arguments that make use of deductive reasoning to form arguments. There are many different types of syllogisms. They are structured in a simple way with two premises and a conclusion in their most basic form.

We have an innate penchant to argue about things. Anyone reading this knows how amazing it can be to verbally wrestle with your friends about why your favorite football club is the best of all time, or perhaps you get into the classic argument of how Marvel’s cinematic universe kicks DC out of the park every time.

As entertaining as arguing can be, having proper arguments to support your beliefs not only helps you defend them, but also helps you form well-rounded opinions. Having the ability to reason by logic is a method that philosophers have used for centuries to determine the true nature of things, to separate idiosyncratic beliefs from true reality.

Human head with maze inside and colorful jigsaw puzzle pieces. Concept of logical thinking, intelligence, mental capacity, mind game(Andrew Krasovitckii)s — Logical thinking is paramount to deduce knowable facts and weed out the false claims (Photo Credit : Andrew Krasovitckii/ Shutterstock)

Logic and deductive reasoning are the pillars of every verifiable fact that we know about this world, helping us navigate through a sea of false claims and beliefs, especially in today’s world, which is so overloaded with information.

Syllogisms are one way to test existing claims and also arrive at new ones.

Recommended Video for you:

Is Mathematics INVENTED or DISCOVERED?

Logical Arguments And Deductive Reasoning

It’s important to determine the degree of truth in a statement and see if it holds any value or if the conclusion it comes to is valid. To do this, we form a series of statements that convey our ‘premises’, which are the known facts or assumptions we make in order to reach a conclusion. This series of statements is called an argument and a logical argument is one in which the conclusion holds true, given the premises.

For example:

All men are mortal (1^st premise)

Socrates was a man (2^nd premise)

Thus, Socrates was mortal (Conclusion)

Here we have used ‘deductive reasoning’, or top-down logic, to reach a valid conclusion by comparing two true premises. This can be done in many ways through various types of logical arguments; syllogisms are one of these arguments, one that uses deductive reasoning to reach a conclusion based on two or more premises that are assumed to be true.

Syllogism And Its Structure

A syllogism is a deductive tool that can be traced all the way back to Aristotle. It has been used by many notable philosophers and was also completely accepted by George Boole, who is famous for introducing Boolean algebra and is also credited for laying the foundation of the information age.

Aristotle watercolor vector portrait with ink contours( Marusya Chaika)s — The use of syllogisms can be traced all the way back to Aristotle (Photo Credit : Marusya Chaika/ Shutterstock)

The basic structure of syllogisms is a three-step process to reach a conclusion using two true premises. These three steps are:

Major Premise

Each part of the argument is a categorical proposition, meaning that it agrees or denies that the instance of one category (the subject or the middle) is part of another category (the predicate). A major premise then becomes the first assertion or claim that you put forward on which to base your argument, which is assumed to be true.

For example:

Some cats are orange: Cats – middle (M) and Orange – predicate (P)

Minor Premise

This is the second assertion that is assumed to be true. It also follows the pattern of a categorical proposition.

For example:

Some mammals are cats; Mammals – subject (S), and Cats – middle (M)

Conclusion

By assuming the two premises are true and comparing the two, we can come to a logical conclusion. This conclusion holds true because both of our premises hold true; it would become invalid as soon as any one of the premises is proven to be false.

For example:

Major premise – Some cats are orange

Minor premise – Some mammals are cats

Conclusion – Some mammals (S) are orange (P)

Various Types Of Syllogisms

As we have seen above, a syllogism takes a form as:

M – Middle, S-Subject, P-Predicate

All M are P – becomes the structure of a Major Premise

All S are M – becomes the structure of a Major Premise

All S are P – becomes the structure of a Conclusion

By using these variables, there are an infinite number of syllogisms, but there are 256 distinct types and 24 valid types of syllogisms.

Furthermore, the premises and conclusions are of one of the following 4 types:

Quantifier	Subject(S)	Copula	Predicate(P)	Code	Type	Example
All	S	are	P	SaP	universal affirmative	All cats are mammals
No	S	are	P	SeP	universal negative	No cats are amphibians
Some	S	are	P	SiP	particular affirmative	Some cats are orange
Some	S	are not	P	SoP	particular negative	Some cats are no feral

These 4 types can be used as either the premise or conclusion within a syllogism. Their permutation and combinations can be infinite, but we will look at 5 common examples:

Barbara (AAA-1)

This type uses universal affirmatives in all the premises and the conclusion. For example:

All animals are mortal (MaP)

All dogs are animals (SaM)

All dogs are mortal (SaP)

Modus Barbara — Venn diagram showing Barbara AAA1 (Photo Credit : Watchduck /Wikimedia Commons)

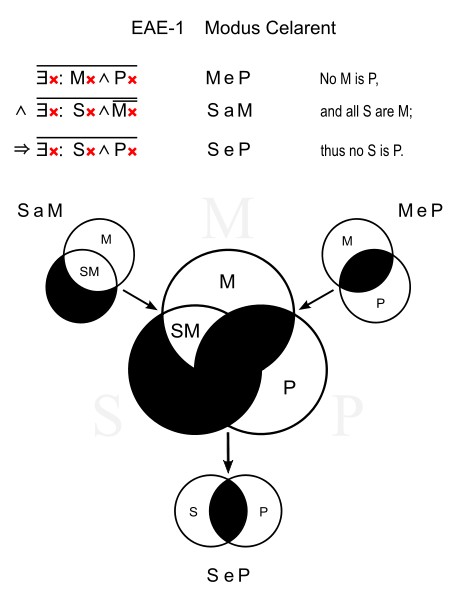
Celarant (EAE – 1)

This type uses universal negatives in the 1^st premise and the conclusion as a universal negative and a universal affirmative in the 2^nd premise. For example:

No human has been to Mars (MeP)

All Indians are human (SaM)

No Indian has been to Mars (SeP)

Modus Celarent — Venn diagram showing Celarant EAE1 (Photo Credit : Watchduck/Wikimedia Commons)

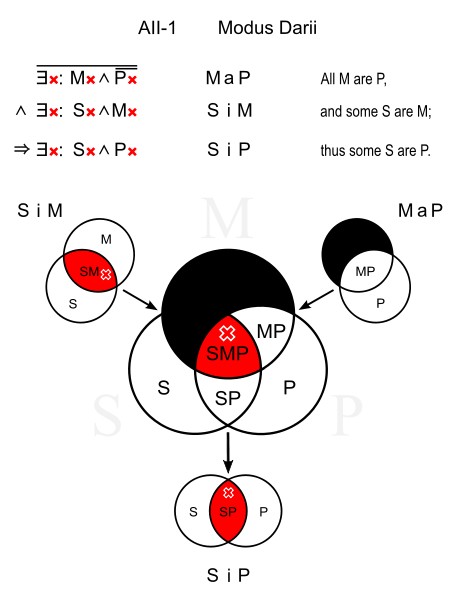
Darii (AII-1)

This type uses the universal affirmative in the 1^st premise and the particular affirmative in the 2^nd premise and the conclusion. For example:

All dogs have tails. (MaP)

Some pets are dogs. (SiM)

Some pets have tails. (SiP)

Modus Darii — Venn diagram showing Darii AII-1 (Photo Credit : Watchduck/Wikimedia Commons)

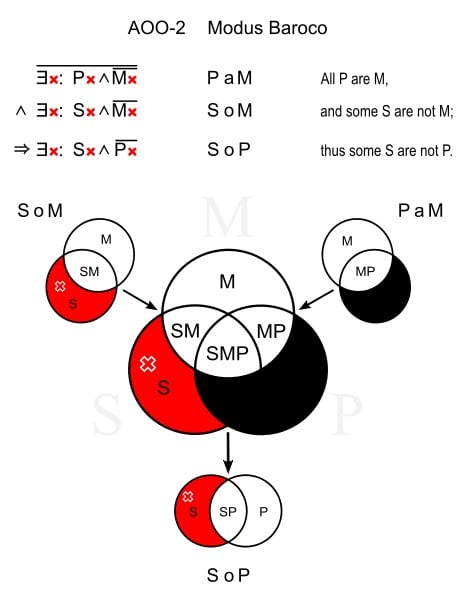
Baroco (AOO-2)

This type uses a universal affirmative in the 1^st premise and a particular negative in the 2^nd premise and the conclusion. For example:

All pets are domesticated. (PaM)

Some cats are not domesticated. (SoM)

Some cats are not pets. (SoP)

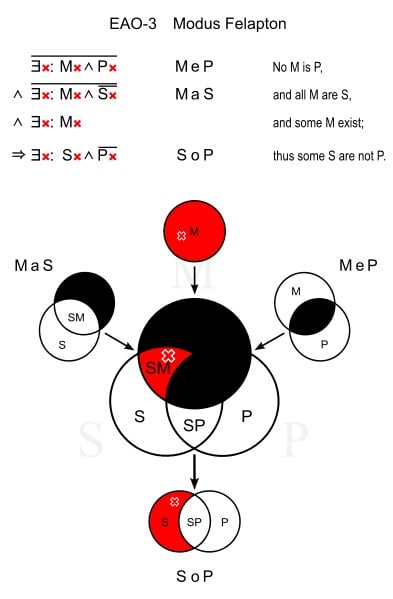
Modus Felapton — Venn diagram showing Baroco AOO-2 (Photo Credit : Watchduck/Wikimedia Commons)

Felapton (EAO-3)

This type uses the universal negative in the 1^st premise, universal affirmative in the 2^nd premise and particular negative in the conclusion. For example:

No mammals are insects. (MeP)

All whales are mammals. (MaS)

All whales are not insects. (SoP)

Conclusion

Syllogisms are an important concept to make any argument better or break down an existing claim to see if it holds true. The verification for this is done through checking the validity of the premises, meaning that you check whether they are true or fabricated, whether the sources of the premises are legit and whether the conclusion is drawn from the true premises.

You don’t need to remember all the various combinations of syllogisms; understanding the basic structure will do the trick when it comes to forming your own unique logical argument. Basically, don’t take any information that comes your way at face value. Break down the premises, conclusions and keep yourself logically informed!

References (click to expand)