What Are Quantum Numbers? What Are The Rules For Electron Configuration?

Quantum numbers are a set of four numbers that define the position of each individual electron in an atom. The first quantum number, or principal quantum number, denotes the number of the shell in which the electron can be found. The second quantum number, azimuthal quantum number, denotes the subshell in which the electron can be found. The third quantum number, magnetic quantum number, gives information about the atomic orbital of the electron. The fourth quantum number, spin quantum number, gives information about the spin of the electron.

The electron configuration of an atom is, in simple terms, the arrangement of electrons around the nucleus of that atom. However, technically, it is impossible for us to state precisely where the electrons will be. Therefore, electron configuration is honestly our best calculated guess as to where the electrons can be found.

This is what a typical electron configuration of an element looks like : Na – 1s² 2s² 2p⁶ 3s¹

The numbers and letters together give the address of each electron, so to speak. Knowing the electron configuration of an atom can provide a lot of insight into its location on the periodic table, predict its behavior in reactions, its state, etc. Let’s try to understand what these are, and determine how to arrive at the electron configuration of an atom.

Recommended Video for you:

Quantum Numbers

These are a set of 4 numbers that together define the position of each individual electron in the atom.

Principal Quantum Number

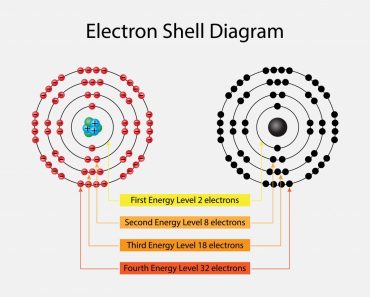
This is denoted by ‘n’. As we know, electrons can be arranged in different shells or energy levels. These are arranged in increasing order, i.e., the shell closest to the nucleus has the lowest energy, which increases as it moves away from the nucleus. In lieu of this, the first quantum number, or principal quantum number, denotes the number of the shell in which the electron can be found. For Na, 1, 2 and 3 were the principal quantum numbers. The first shell, i.e., n=1 is called the ‘K’ shell, while n=2 is called the ‘L’ shell and so on and so forth.

Azimuthal Quantum Number

Denoted by ‘l’, this is also called the orbital angular momentum quantum number. These values start from 0 and keep increasing. This number has 2 functions – it states the subshell in which the electron can be found, and also gives us an idea of the shape of the orbital. The value of l depends on the value of n. Values of l can range from 0 to n-1 and are always positive integers. For instance, if n=3, l=0,1,2.

As mentioned, these values can also tell us the shape of the orbitals. When l=0 corresponds to the s subshell, l=1 corresponds to the p subshell, l=2 corresponds to the d subshell, etc. The concept of subshells is not that complicated. Just as shells are based on varying energy levels, subshells work much the same way. Within each shell there also exist different energy levels. The difference in these energy levels isn’t enough for it to qualify as a separate shell, so they have been classified as subshells.

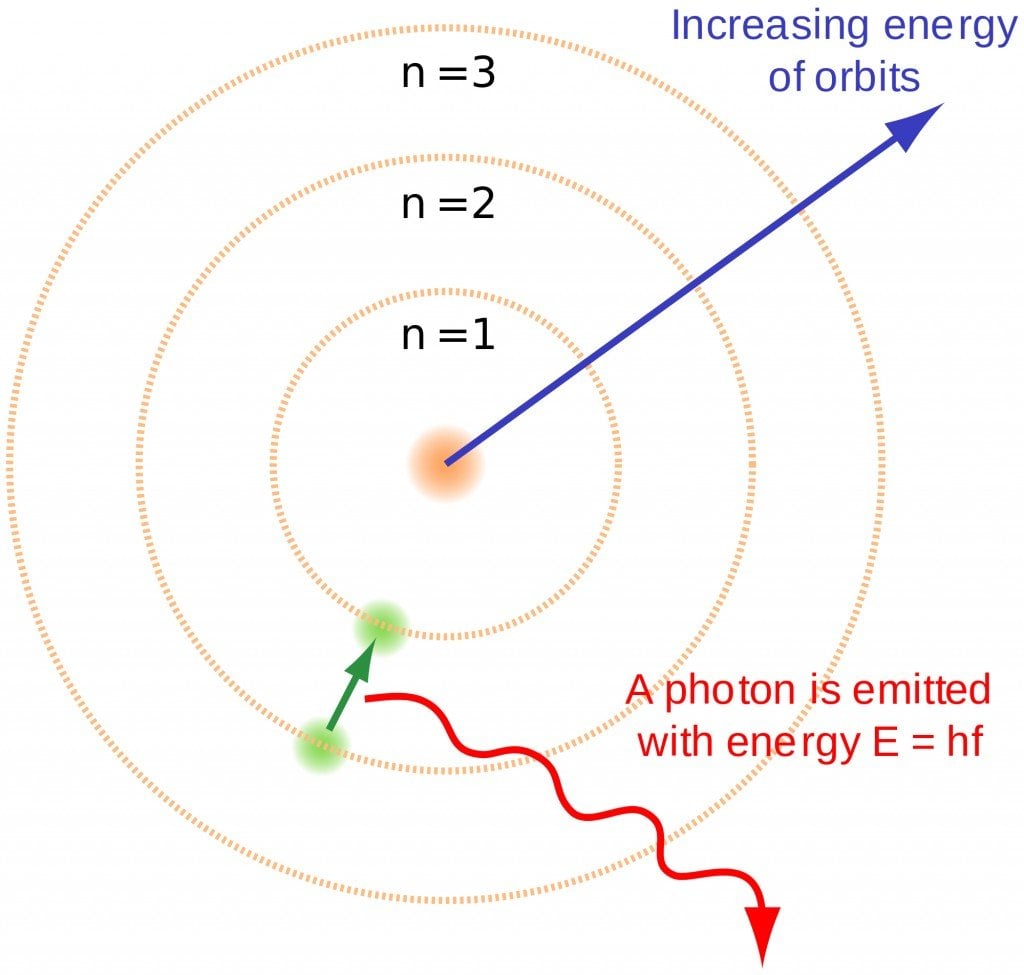
Magnetic Quantum Number

This number, denoted by ‘m’ gives information about the atomic orbital of the electron. Think of atomic orbitals as electron containers that can hold up to a maximum of 2 electrons. The subshells have these containers in which electrons are present. The whole thing can be imagined by a simple example. Think of shells as different streets. Each street has a number of buildings – the subshells. Within each building are apartments, which are the orbitals. People are the electrons. There can be maximum of 2 people in an apartment, and obviously, the people can only stay in apartments.

The value of m depends on the value of l. The number of orbitals range from –l to l for a given value of l.  For instance, when l = 1, m = -1,0,+1. Keep in mind that -1, 0 and +1 only give the number of orbitals, and not their name. For l=1, the subshell is p. The orbitals in p are p_x, p_y and p_z.

Spin Quantum Number.

This is the easiest of the numbers to understand. As we know, electrons are constantly spinning, which leads to the generation of a magnetic field around them. This quantum number, denoted by s, gives information about the spin of the electron. It has 2 values, +1/2 and -1/2 which are the types of spin an electron can have.

These four quantum numbers essentially function as the address of the electron. However, there are certain rules to be followed when assigning them.

Aufbau Principle

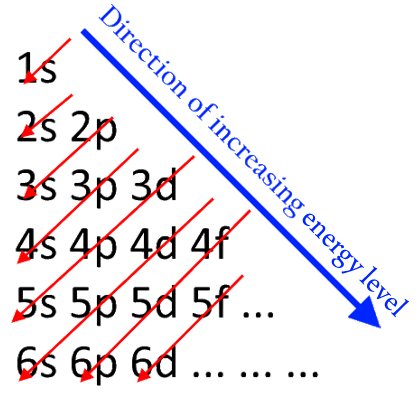
This principle says that when electron shells are being filled, or when electrons are being assigned to their orbitals, they will start filling from the lowest energy level and then keep increasing. This means that the first electron cannot be in the 2p_x orbital. It must start from the 1s orbital and keep moving up. One would expect the electrons to first fill up the orbitals of all the subshells of one shell, and then move on to the next. However, due to certain factors, that is not quite so. The order of the energy levels of the shells is slightly different, which is shown in the image below.

Hund’s Rule Of Maximum Multiplicity

When we think of the p subshell of a shell, it has three orbitals – x, y and z. All these orbitals are of the same energy. Hund’s rule says that when filling up degenerate orbitals, or orbitals of the same energy, the electrons will first fill each orbital singly, and then the second electron will be added. This means that if 4 electrons are to be added to the p subshell, x and y orbitals getting 2 electrons each and z getting no electrons will not happen. Rather, each orbital will first be given one electron, and then, depending on how many electrons are available, they will be given a second one. Therefore, x will get 2 electrons, while y and z will get one electron each.

Pauli’s Exclusion Principle

According to this principle, no electron can have all four of the same quantum numbers. As we know, the first three quantum numbers give the location of the electron up to the orbital, while the fourth one provides the spin of the orbital. Therefore, if 2 electrons occupy the same orbital, they must have opposite spins. Obviously, if the electrons had the same spins, there would be too much repulsion between them for them to remain in the same orbital.

Using the number of electrons in an atom, which is equal to the atomic number, one can assign electrons to the orbitals, keeping all these rules in mind. For instance, oxygen has 8 electrons. Going over the rules, one can calculate that the s subshell can accommodate 2 electrons, p can accommodate 6, d can hold 10, f can hold 14, and so on. Therefore, the configuration of oxygen will be 1s², 2s², 2p⁴