Table of Contents (click to expand)
Life on earth was not always as we find it today. Billions of years ago, a massive change in the oxygen levels around earth changed it’s history forever.
Are you done with the polluted air of your city and instead want to live in a fresh, oxygen-filled atmosphere like Earth had before any of our gas-leaking machines were invented? Some people think that a time machine would quickly solve the problem, taking us back to the years when our beautiful planet was forming. If you also hold any such ideas, see if you still believe them after reading this article…
What if you traveled back in your time machine billions of years only to find there was no oxygen on our planet? That would not be the best welcome to an ancient era. However, on a more serious note, there was a time when this life-nourishing molecule was not found in our atmosphere. A specific series of events are responsible for the present composition of the air that we breathe. Let’s take a closer look!
Recommended Video for you:
What Is The Great Oxygenation Event?
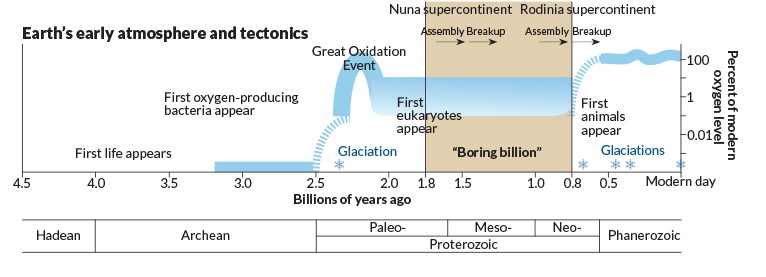
The great oxygenation event, also known as the oxygen catastrophe, was an event that saw a massive surge in the oxygen concentration in Earth’s atmosphere and the oceans below it. This occurred during the Proterozoic eon (Earth’s life span is divided into four geological eons or time regions for better understanding), about 2.5 billion years ago, when Earth’s atmosphere was not the oxygen-rich mixture that we breathe today. Instead, it was made up of nitrogen, methane and carbon dioxide. All the oxygen was locked up in water molecules, which covered most of the surface of the planet.
Now, you may be wondering how life survived in such an environment… Well, it survived because most of it was composed of anaerobic life forms that thrived in the absence of oxygen, scavenging whatever molecules they could find inside the oceans. Somewhere around 3-3.5 billion years ago, one of these microbial species decided to swim to the surface and get a taste of life around there. It was during this period that these organisms learned how to harness the power of sunlight and combine it with molecules of carbon dioxide and water to generate energy and sugar, in addition to releasing oxygen as a by-product, a critical process we now call photosynthesis.
What Role Did Cyanobacteria Play?
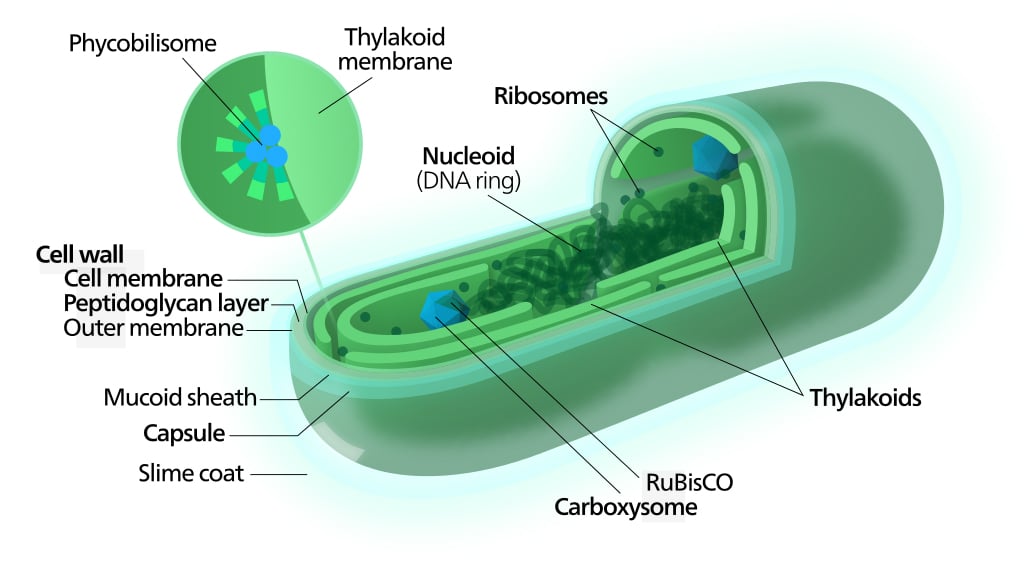
These bacteria were the ancestors to the somewhat more complex organisms today known as cyanobacteria. Have you ever heard this term before? These blue-green species are found everywhere, from the heights of space to the bottom of the oceans. Photosynthesis was a major boost for this species, as they started multiplying at a tremendous rate, filling (practically polluting) the atmosphere with oxygen. This was not great news for the anaerobic life forms, as oxygen-rich air was actually toxic to them. As a result, about 2.5 billion years ago, all the life on Earth went extinct; the cyanobacteria barely survived. This period, in particular, is known as the oxygen catastrophe.
The driving force that pushed unicellular organisms to turn into multicellular ones is still debatable, and many researchers claim that it was the massive oxygen release that prompted the photosynthesizing bacteria to turn relatively more complex. As life evolved on all fronts, including size, the smaller cyanobacteria were swallowed by certain larger organisms, which provided those larger organisms with the ability to photosynthesize. Evolution theory suggests that the cells of these organisms went on to form the basis of the plant cells, while the cyanobacteria inside them turned into what we today call chloroplast.
The Huronian Glaciation
Given that cyanobacteria had an endless supply of resources, they kept increasing in number, releasing more and more oxygen into the atmosphere.

When the oceans became saturated, the life-giving gas left the water and entered the air, increasing its concentration further. The excess oxygen reacted with the methane present in the atmosphere to form water and carbon dioxide, neither of which retain heat as well as the greenhouse gas, methane. This changed the climate of our planet drastically, covering it in ice for hundreds of millions of years. This period has come to be known as the Huronian Glaciation era.
This was the longest ice age that our planet witnessed, and it lasted for about 300-400 million years. When the Huronian Glaciation ended, some 2.1 billion years ago, some life prevailed, and it inherited a better and more hospitable planet—most importantly, an atmosphere with plenty of oxygen—all at the expense of their ancestors. Following that, the oxygen levels in the air continued fluctuating before settling on its present value of 21% by volume. However, the way humanity is proceeding with its affairs, this number may not be valid for long.
A Final Word
The first inhabitants of Earth died by suffocating in the gas released as their own waste product. Now, this doesn’t sound right, initially, but it goes on to teach a fundamental lesson: things usually get worse before getting better, and life is no exception. An essential lesson that we can take from this is that oxygen was formed at the expense of billions of creatures, and if we don’t stop polluting the oxygen we have, this miraculous gas won’t hesitate to wipe out a few billion more.
What eventually formed the basis of all complex life on Earth could have gone terribly wrong, possibly destroying every organism on the planet. Fortunately, it did not, and here we are. The great oxygenation is perhaps the most important event in the history of our planet that affected all life forms in such a profound way.
References (click to expand)
- Bekker, A. (2014). Huronian Glaciation. Encyclopedia of Astrobiology. Springer Berlin Heidelberg.
- The Great Oxygenation Event – when Earth took its first breath - blogs.unimelb.edu.au
- Great Oxygenation Event - an overview.
- Schirrmeister, B. E., Gugger, M., & Donoghue, P. C. J. (2015, June 23). Cyanobacteria and the Great Oxidation Event: evidence from genes and fossils. (A. Smith, Ed.), Palaeontology. Wiley.












