“The two most common elements in the universe are hydrogen and stupidity.” ~ Harlan Ellison
What is the most common thing between fans of Lionel Messi and Cristiano Ronaldo?
It’s not their love and crazed affection for their icons, but rather HYDROGEN.
Hydrogen makes up around 10% of the human body by mass. It is present in the form of water and other organic molecules throughout the body.
So, what we all have in common is hydrogen.
The first element of the periodic table and the most abundant chemical substance in the universe, Hydrogen derives its name from Greek— “hydro” meaning “water” and “genes” meaning “former” — given by the French chemist Antoine Lavoisier. It is found in 75% of all common matter. Its atomic number (the number of protons present in the nucleus) is 1. It normally exists in its gaseous state under standard conditions. It is a colorless, odorless, and highly combustible element.
The pure form of hydrogen is scarcely present in the Earth’s atmosphere because it escapes the Earth’s gravity quickly, as suggested by some studies. It is mainly found combined with oxygen and water, as well as in organic matter.

There are three naturally occurring isotopes (atoms of the same element having the same atomic number, but different mass numbers) namely Protium (¹H), Deuterium (²H), and Tritium (³H). A fun fact is that hydrogen is the only element whose isotopes have different names that are commonly used. Surely, this element holds a special status in the field of Science!
Recommended Video for you:
How Was Hydrogen Discovered?
In 1671, Robert Boyle produced hydrogen gas while studying the reaction of iron with acids, but he didn’t initially recognize it.
Later, in 1766, Henry Cavendish recognized hydrogen as a distinct element when he conducted an experiment with zinc and hydrochloric acid. He collected the bubbles of the gas and showed that it was of a different gas, one that came to be known as hydrogen. Later, he also showed that hydrogen burns in air to form water. This led to the end of the belief that water was an element. Hence, Henry Cavendish is credited with the discovery of hydrogen.
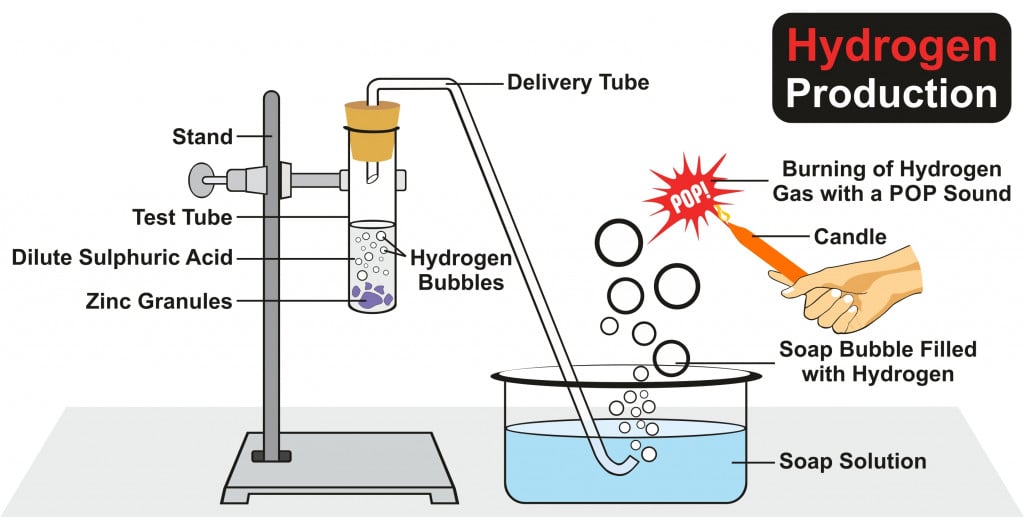
Why Does Hydrogen Burn With A Popping Sound?
Hydrogen is a highly reactive element. This non-toxic gas is highly combustible as well.
When hydrogen undergoes a chemical reaction with oxygen, that is, when it burns in air, it produces a characteristic popping sound.
Let’s explore the reason behind this unusual sound.
When two molecules of hydrogen combine with one molecule of oxygen, they undergo a chemical reaction to produce two molecules of water—and also release a lot of energy. This reaction is therefore exothermic in nature. Hydrogen is also called “water-former” because of this reaction.
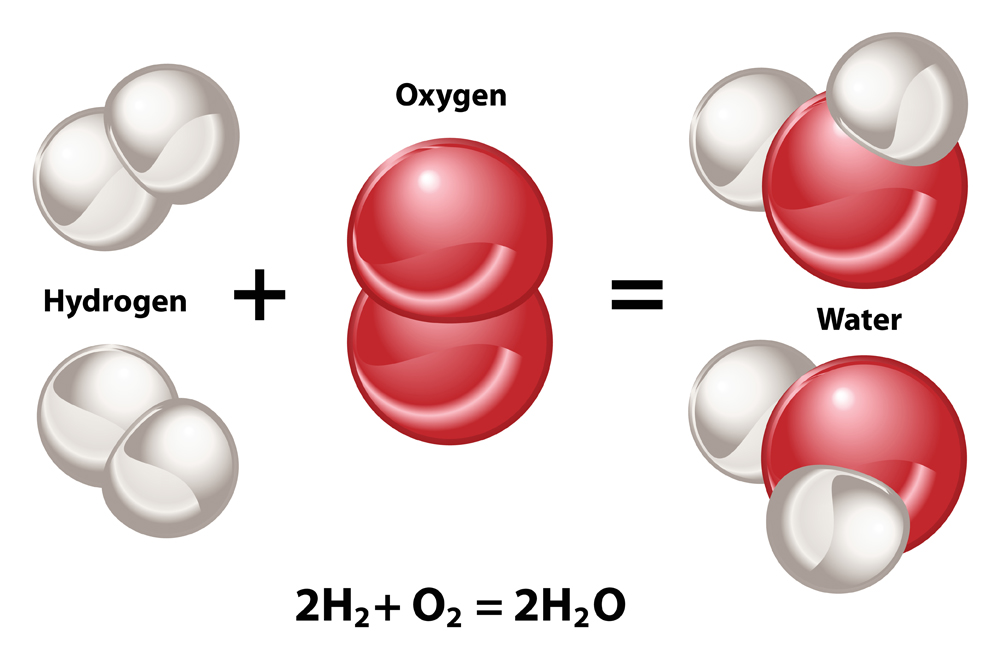
The energy released in this reaction is mostly in the form of heat. This heat imparts kinetic energy to molecules of the gaseous mixture and causes them to expand. The air surrounding the gases also starts expanding very rapidly. This sudden and quick expansion of gas molecules causes a break in the sound barrier. Thus, we hear a pop sound when hydrogen is burned due to the explosion.
The pop sound also results from impurities present in the gaseous mixture undergoing the chemical reaction.
Some Other Reactions Involving The Emission Of Sound
1) The burning of firecrackers emits sound energy due to the explosive chemical reactions of potassium nitrate, sulphur, and carbon into potassium carbonate, nitrogen, potassium sulphate, and carbon dioxide.
2) Usually, a popping sound is heard while lighting an oxy-acetylene torch because of a blockage or leakage of gas flow in the torch.
The Future Of Hydrogen
Recent studies suggest that hydrogen is a promising source of “clean” fuel for the Earth. Its great abundance in the universe is an added advantage for us. It is already powering the universe through stellar hydrogen fusion processes and proton-proton reactions, just to name a few.
Hydrogen can very effectively serve as a pollution-free fuel, as it has no molecules of carbon in it. It produces water when burned. A tremendous amount of energy can be harnessed from chemical reactions involving hydrogen that could solve the problems of energy deficiency.

However, it’s not always easy to achieve a great feat. The same is the case with harnessing hydrogen for our benefit. Hydrogen fuel is expensive, which is a major drawback, since industries prefer cheaper fuels. Also, the current process to produce hydrogen itself is not so “clean” or “pollution-free”. Hydrogen for industrial use is mostly produced from natural gas, which generates carbon dioxide (CO2).
Researchers have been working towards finding alternative and more environmentally friendly ways for the mass production of hydrogen. If humankind is successful in discovering and inventing better methods of hydrogen production that would be cost-effective, as well as cleaner and greener, then hydrogen could quench our thirst for unlimited energy for generations and generations. Hopefully, this day isn’t too far away!













