What Is The Relationship Between Thermodynamics And Statistical Mechanics?

In the field of science, particular equations play an important role in establishing the relationship between two branches. For example, the Boltzmann’s Equation is the bridge between Thermodynamics and Statistical Physics.

There are often two sides to a particular story, and the arena of science is no exception to this adage.

Generally speaking, Thermodynamics and Statistical Mechanics try to solve similar problems, but from different points of view. The former does so at the macroscopic level, while the latter operates at the microscopic level.

Thermodynamics deals with the relation of heat, work, pressure, and temperature with other forms of energy, as well as the physical parameters and properties of a material.

Statistical mechanics, on the other hand, applies statistical and probabilistic methods to establish the behavior of the atoms and molecules of a gas (in general).

It’s fair to say that these two branches of Physics have a broad area that overlaps with each other, with statistical mechanics arising as a result of developments in classical thermodynamics. So, it’s quite obvious that there must be a relation between the two. Let’s try to understand this link from the bottom up!

Recommended Video for you:

The Concept Of Entropy

Entropy is a very important concept of thermodynamics, introduced by Rudolf Clausius, a German physicist, in 1850.

In general, entropy denotes the amount of disorderliness of a system under consideration. It is often associated with the concept of uncertainty in a system. It is a state function, meaning that its value depends upon initial and final positions that the state follows, but not on the path. It is also an extensive quantity, which means that it is proportional to the amount of substance taken into consideration.

Specifically speaking, entropy is a measurement of the molecular disorderliness or randomness of a system, which plays an important role in determining the properties of the system.

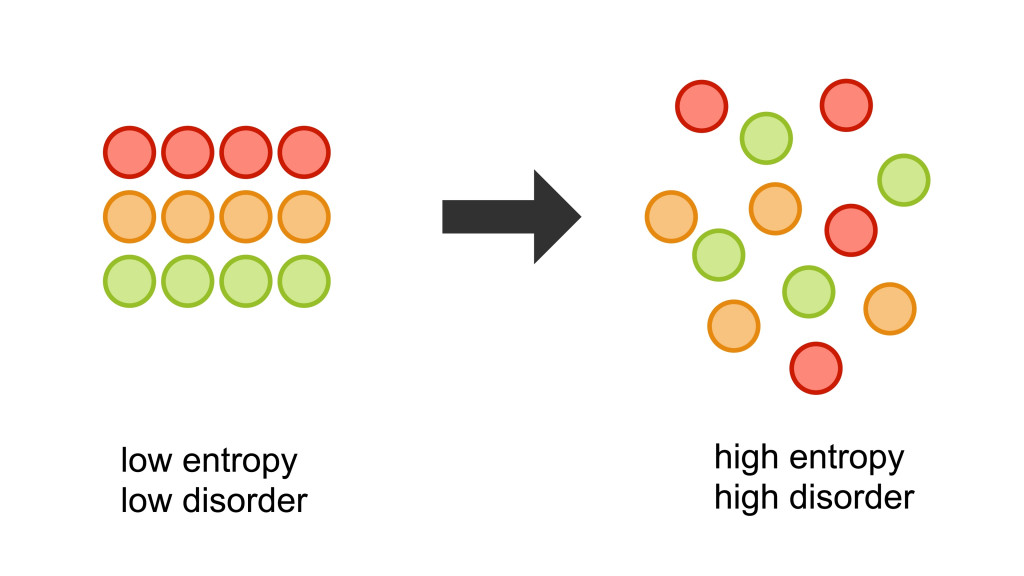
It is interesting to note that Entropy can be the answer to why your life gets more complicated as time passes, rather than getting easier. Now you know what to blame!

As suggested by the Second Law of Thermodynamics, the total entropy of an isolated or closed system always increases or remains constant, but never decreases. This law holds a special place in both Thermodynamics and Statistical Mechanics.

The Concept Of Microstates

Two terms are widely used in Statistical Mechanics, namely macrostate and microstate.

A microstate is a specific configuration of all the molecules of a system in terms of energy, momentum, and position. A macrostate is the collection of all the possible microstates of a system with the same thermodynamic quantities, like temperature, volume, pressure, number of molecules, etc.

In statistical mechanics, researchers are mainly concerned with the microstates of the system, as their detailed study reveals the nature of the system, microscopically. This in turn is useful in determining the entropy. We can also approximate the macroscopic behavior of a system through averaging the behavior of the corresponding microstates under the same conditions.

Microstates also form the basis for many calculations and results derived from Statistical Mechanics.

The Boltzmann Equation – The Relation That Connects Both

Since both Thermodynamics and Statistical Mechanics have some common ground, a particular relation forms a bridge between the two. This equation relates thermodynamic entropy with the statistical entity of a microstate, for an ideal gas, as follows:

S= K log W

This equation is known as Boltzmann’s Equation or the Boltzmann-Planck equation.

Here, S denotes the entropy, W denotes the number of microstates corresponding to a particular macrostate of the gas, and K refers to Boltzmann’s Constant, equal to 1.380649 × 10⁻²³ J/K.

The equation was formulated by an Austrian Physicist, Ludwig Boltzmann between 1872 and 1875, and was later corrected in 1900 by Max Planck, a German Physicist, to give it its present form.

Interestingly, Boltzmann’s Equation relates the classical world with the world of probabilistic approach through this simple-looking equation. This equation has come to be known as a staple of science due to the interconnection it establishes between microstates and macrostates.

Einstein’s Criticism Of The Equation

In 1904 and after, Albert Einstein became quite skeptical of Boltzmann’s Equation and continuously criticized it. He was of the view that the equation had no valid theoretical evidence and regarded it as incomplete. He stated that the complete molecular-mechanical theory for the calculation of ‘W’ wasn’t mentioned. However, he couldn’t come up with an alternative to this formula. Therefore, scientists and physicists around the world continue to use the Boltzmann Equation.

Though Statistical Mechanics and Thermodynamics are considered separate branches of Physics, both are governed by the same four laws of Thermodynamics—the Zeroth, First, Second, and Third Law.

The microscopic world, the human body, and the whole rest of the universe abide by these laws in one way or the other. How cool is it that laws conceived by humans seemingly govern the whole universe!

A keen eye for detail, a sensitive ear, and an analytical brain are a blessing to humankind in our pursuit of unveiling universal mysteries! Keep your curiosity glasses on at all times!