Table of Contents (click to expand)
The mathematical logic behind the different A-size papers is that they are all based on the German DIN 476 standard for paper sizes. This standard is based on the ratio between the length and width of the paper. All A-size papers have the same ratio between their length and width, which is 1.414. This allows for easy scaling of content from one size to another without losing symmetry.
A4-sized paper has become a staple of stationary, both in offices and households, all over the world (except the United States). Given its immense popularity, the A4 size has become the standard business letter size in countries like United Kingdom and New Zealand. A3 and A2 sheets are relatively less common, and the A1 and A0 variants even more rare.

Such standardization of paper was first introduced in the 20th century and is ascribed to all over the world to this day. So, what’s the difference between different A-sized sheets and how are they standardized?
Recommended Video for you:
A-Series Sheets
To give a little background, the international paper size standard is ISO 216, which specifies the international standard (ISO) paper sizes used in most countries in the world today. It is based on the German DIN 476 standard (DIN is a German organization for standardization) for paper sizes. The most popular ISO standards of paper include A, B and C-series sheets, but in this article, we’re going to talk about the most commonly used variant: the A-series.
What’s So Special About A-sheets?
A-series sheets of paper have been designed in such a way that when you cut them in half, you get two perfectly identical pieces of the next biggest size. For example, if you cut an A0 sheet in half, you will get two A1-sized sheets; if you cut an A1-sized sheet in half, you will get two A2-sized sheets and so on.
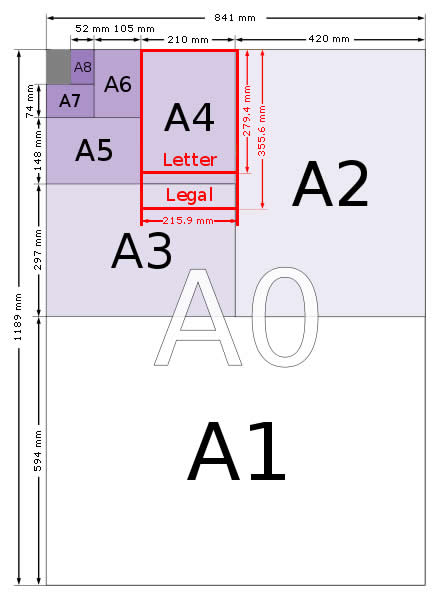
Although the dimensions of the two new sheets are different from their parent sheet, the proportion of the sheets’ length and breadth remains the same. Therefore, when you fold an A3 sheet in half, you get two A4 sheets that have the same ratio between their length and breadth as the parent (A3) sheet.
How Do You Determine The Exact Dimensions Of A-sheets?
As mentioned above, all A-standard sheets have the same ratio between their length and breadth. That being said, what’s the value of that ratio, and how does it remain constant for all A-standard sheets?
To answer this, we’ll have to go back to where it all started: the first sheet of paper that was officially standardized by putting the letter ‘A’ as a prefix to its name was the ‘A0 sheet’. An A0 sheet is exactly 46.8 inches long and 33.1 inches wide (841 mm x 1189 mm) and has an area of 1 meter squared. Now, if you divide 1189 by 841 (i.e., the dimensions of an A0 sheet) you get 1.414. What’s so special about this number, you ask?
Well, the dimensions of every A-standard sheet, if you care to check the math, are in the proportion of 1.414, which also happens to be the value of ….
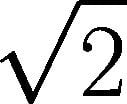
Given below are the dimensions of different variants of A-standard sheets:
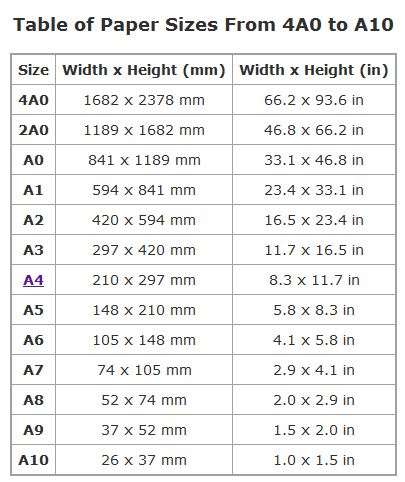
You can see that, whether it’s an A8 sheet or an A0 sheet, the ratio (1.414) between the length and breadth remains the same. The beauty of such well-defined distinction is that you can easily upscale/downscale your content (including images, text etc.) to bigger/smaller sheets without losing its symmetry.
Had the ratio of the different A-standard sheets not been fixed, the transfer of content from one size to another wouldn’t be so simple and flexible. Since the ratio of sides of all A-standard sheets is 1.414, you can easily expand a document to its next biggest size by dialing in a factor of 141% in a machine. This tip comes in handy while working on various photo-editing tools, photocopying documents and so on. Also, you can easily convert one bigger A-size sheet to the next two A-sized sheets.
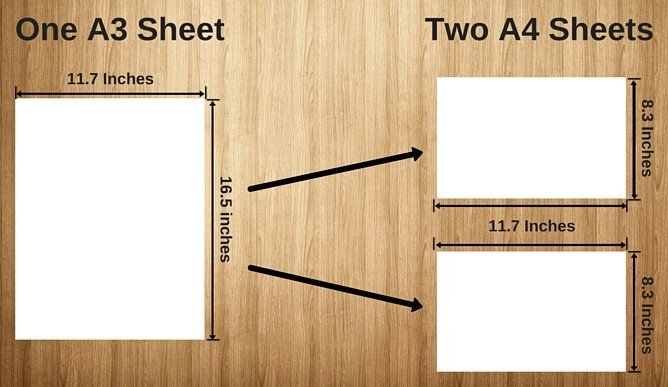
For instance, you can divide an A2 sheet to make two symmetrical A3 sheets, two A3 sheets to make four symmetrical A4 sheets, etc.
Who would have thought that such a simple – yet ingenious! – technique using mathematics could be used to regularize the dimensions of sheets of paper all over the globe!













