Table of Contents (click to expand)
Most planets in our solar system have elliptical orbits rather than circular orbits. This is because their orbits are affected by the gravitational interactions of other planets and stars. An elliptical orbit is more likely to be disturbed than a circular orbit. However, a planet’s orbit can become more circular after a collision with another planet or astronomical object.
For many children, a popular science project consists of making dioramas of the solar system, with painted styrofoam balls for planets and orbital paths made of wire. To this day, when most adults think of the solar system, they imagine a group of concentric rings, with the furthest planets on the largest circular ring and the Sun smack-dab in the center.
While that makes for a neat and tidy project, it isn’t exactly correct in reality. The orbits of the planets in our solar system (and the vast majority of planetary objects in space) are not perfectly circular. Planets have orbital eccentricity which makes the orbit a little more stretch, technically called an ellipse. Now the question arises how stretch are these elliptical orbits and why?
Recommended Video for you:
Orbital Eccentricity
An ellipse is symmetrically shaped closed oval. It has two points called foci around which it is constructed. These foci act as a combined center for the ellipse.
When it comes to planetary motion, orbital eccentricity can give a lot of clues about the nature of the motion or spin. The orbital eccentricity of a planetary body is a parameter that tells how much its orbit deviates from a perfectly circular orbit. In other words, orbital eccentricity tells how flat or round the path of orbit could be. The value of eccentricity varies between zero and one; with zero representing circle and one transforming into a parabola.
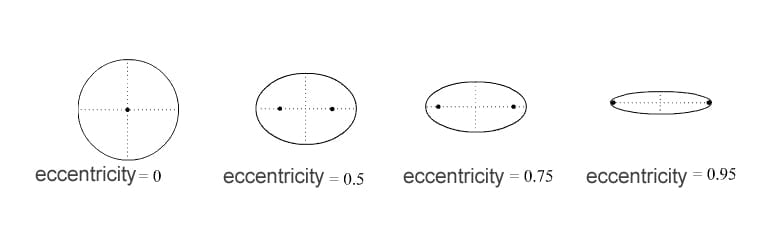
The circle is a special case of ellipse wherein the two foci are exactly at the same point. So, the eccentricity of the circle is zero. As the foci start to separate, the more elliptical or ovular the path of revolution becomes.
More circular orbits have a value closer to zero while highly elliptical ones have a value approaching close to one. The orbital eccentricity of different planets in our solar systems is given in the table below:
| Planet | Orbital eccentricity |
| Mercury | 0.206 |
| Venus | 0.007 |
| Earth | 0.017 |
| Mars | 0.093 |
| Jupiter | 0.048 |
| Saturn | 0.056 |
| Uranus | 0.047 |
| Neptune | 0.009 |
As seen from the table, it is pretty evident that most of the planets are very close to a circular path. Although Mercury is relatively more elliptical than the rest, still it is more close to zero than one, meaning closer to a circle than an (extreme) ellipse. Our own planet Earth has an eccentricity of 0.017 which is almost circular and to the naked eye. A slight elliptical bulge wouldn’t be noticeable. Venus, the Earth’s twin, has its orbit even more close to a circle with eccentricity as low as 0.007.
So Why Aren’t They Perfectly Circular?
It was long thought that all orbits are fully circular because that was considered an ideal shape until the Kepler came in and put forth that orbits are slightly elliptical. Well, in an “ideal” Universe, all orbits would have been “circular”. In fact, some orbits are perfectly circular but those instances are very few and far between. Because for a perfectly circular orbit, the orbiting planet would need to have mass, velocity, and distance from the star which precisely matches the gravitational influence of that star. Even if these ideal initial conditions are met for a nice perfectly circular orbit, it’s unlikely to last very long.

If the mass of a star or planet changes or any other celestial body whiz pass that planet, it would disturb this delicate balance of mass, velocity, and distance which keeps a planet in a circular orbit and change it to an elliptical one. A small tweak in this status quo conditions or any interplanetary interactions would change the path from a perfect circle.

So, you see a change in planetary or star composition or even the influence of celestial bodies in the vicinity prevents the planet from revolving in a nice circular orbit. But despite fretting about orbits being not perfectly circular, it is worth understanding these orbits are still close to circular than being highly elliptical.
What If Planets Had Much More Elliptical Orbits?
Planets having highly elliptical orbit are likely to run into more trouble compared to a circular counterpart. Revolving in highly elliptical orbits makes planets more susceptible to gravitational interactions and nasty impacts. You may wonder why? Well, think about it, your planetary model taught in school that consists of those concentric circular paths, naturally stacks over one above the other without crossing the path which each other. But in the case when planets have an elliptical path with different eccentricities, orbits are likely to cross paths with each other.

This makes planetary bodies more susceptible to collision and impacts. In the aftermath of an impact, a couple of things could happen. One is that both the colliding objects could break and dispersed off into pieces after a collision. Or they could simply merge into a single bigger entity. Many astronomers reckon this sort of activity has been happening in our solar system for billions of years. Planets that exist today in our solar system aren’t the only ones that came into being since the inception of our Sun. But they are probably the only a few planets that have endured/escaped these impacts. The nearly circular orbit with which these planets revolve has certainly helped them in their survival.
Saturn As Reference
We just learn that planets with highly elliptical orbits are more likely to encounter collisions with nearby planets or astronomical objects. Interestingly, many astronomers posit that after these collisions, the orbit of the planet tends to get more circular. This can be best witnessed by looking at the rings of Saturn. Countless chunks of particles orbiting in its ring historically have often collided with each other until the orbit gradually carved out to be nearly circular, Now, they bump against each far less frequently.

A Final Word
So, to summarize mass, velocity and gravitational interaction must combine in an impressive fashion for an orbit to be circular. A slight tweak in any of them will make the planet lose its perfectly circular path and turn elliptical. How much elliptical or elongated these ellipses would be the function of change in these initial conditions. Now, when it comes to our solar system, we learn that though no planet has a perfectly circular orbit, most of them are very close to being circular and perhaps that’s the secret of their survival for so long.
References (click to expand)
- What Is an Orbit?. The National Aeronautics and Space Administration
- Why do planets have elliptical orbits? (Beginner) - Curious About Astronomy? Ask an Astronomer - curious.astro.cornell.edu
- Kepler's Laws - Hyperphysics. Georgia State University
- ELLIPTICAL ORBIT. The California Institute of Technology