Table of Contents (click to expand)
The decimal system is favored because we have ten fingers. However, the dozenal system would fare much better. It is more divisible, which makes it easier to divide goods or money. It is also more versatile. The only downside is that it would require rewriting a majority of math textbooks.
The decimal system is widely favored for the simple reason that we have ten fingers. Each abstract quantity from 0-9 can be counted on each of our long fingers. Had our primate ancestors evolved with twelve fingers, perhaps humans would have adopted the duodecimal or Base-12 system for counting. However, this inadequacy in no way stopped us from exploring the option, as well as higher numerical systems.
The Egyptians, in fact, counted not on their ten fingers, but on the twelve joints between their fingers. It is a pity that entire institutions are based on the decimal system, that we still use for our daily, mundane computations, such as counting money when, as mathematicians suggest, Base-12 or the dozenal system would fare much better.
Recommended Video for you:
Higher Divisibility
The twelve symbols in the dozenal system are listed as 0-1-2-3-4-5-6-7-8-9-χ (pronounced ‘dek’) and ε (pronounced ‘el’). The number 10 in the system becomes 12 and is pronounced ‘doh’. The next twelve numbers are listed with the prefix ‘doh’ in this way: doh-1 (11), doh-2 (12), doh-3 (13), …doh-dek (1χ), doh-el (1ε). The number 20 is therefore called 2-doh and the next numbers are listed with the prefix 2-doh, such that 21 is pronounced as 2-doh-1 and so on until you reach 30 or 3-doh.
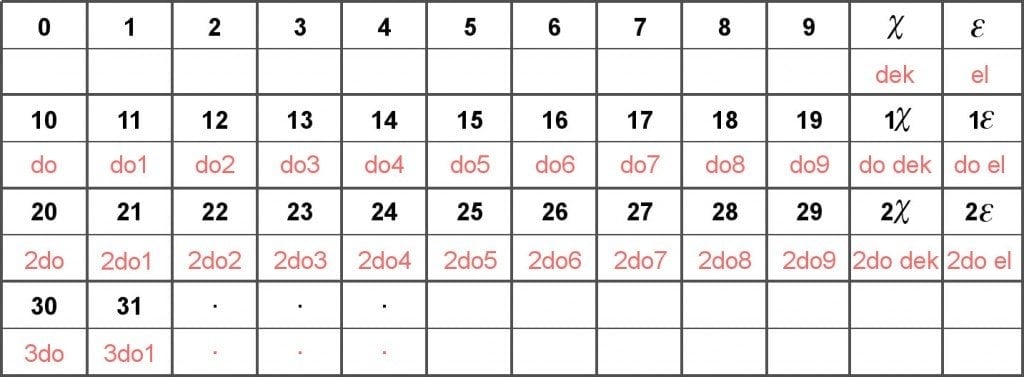
Of course, the system seems bewildering at first, but so does the decimal system or the alphabet to a child encountering it for the very first time. Once we become accustomed to the system, however, we begin to realize that its benefits are worth the trouble. For instance, children will find that learning multiplication tables in Base-12 are much easier than they would be in Base-10. Consider the multiplication tables of three, four and six in Base-12.
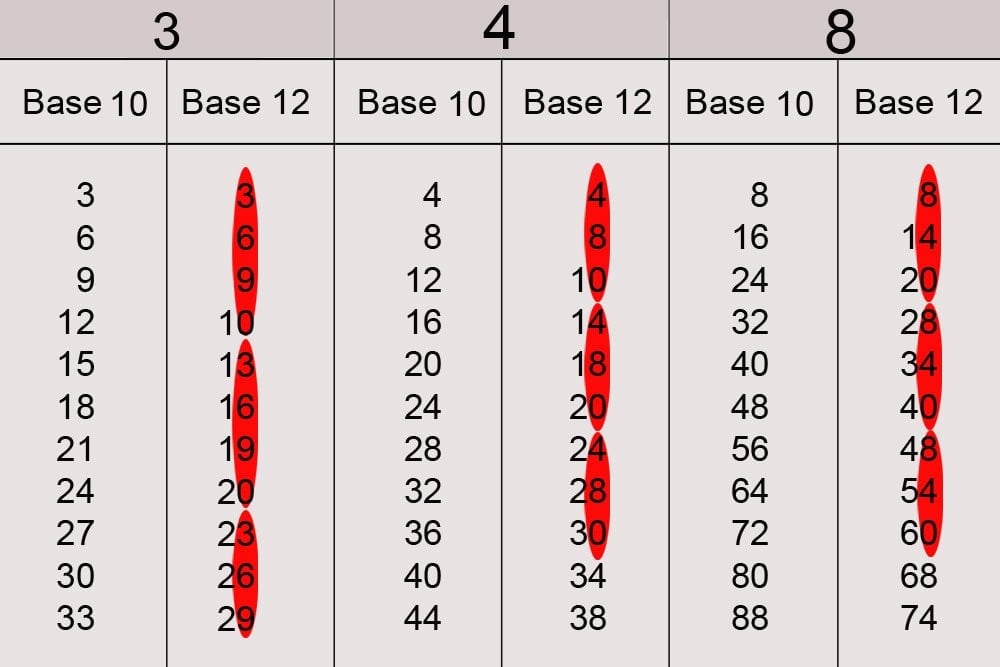
The transformation shows that a distinct, recurrent pattern emerges within each table, rendering them easier to learn.
However, mathematicians don’t admire the system for its aptitude for multiplication, but rather for its aptitude for division. An excellent number system is one that is divisible by more numbers. For instance, while 10 is only divisible by 1,2, 5 and 10 itself, 12 is divisible by 1,2,3,4,6 and 12 itself. This makes for easier opportunities to divide say, goods or the money you buy them with.
Consider dividing $100 or 100 goods into three equal parts. Each part will consist of $33.3333.. or 33.3333.. goods each, a fraction that is universally frowned upon. Now, let’s divide the same number in the dozenal system. Now, 1/3 is the same as dividing 4/12, however, 12 in the dozenal system is 10, so, the division now becomes 4/10, which is equal to 0.4, a perfectly rigid fraction.
Or consider dividing $100 into 2/3 parts. Each part must acquire $0.6666.., again, a number that perturbs us. Now, let’s perform the division in Base-12. The fraction can be written as 8/12, which in the dozenal system transforms to 8/10 or 0.8, a number not so perturbing.

The Most Versatile System
However, one can argue that if divisibility is the virtue of an excellent system, shouldn’t we adopt an even larger system, such as Base-200? The logic is indisputable; 200 is divisible by far more numbers than 10 or 12 is. Also, the space complexity is drastically reduced, as it allows us to represent larger numbers with smaller units. However, to use the system effectively, one must remember a mammoth 200 symbols! On the other extreme, there is Base-2 or the binary system, which consists of merely two symbols (1 and 0) but requires a number as small as 50 to be represented by a long string of bits: 110010. Let’s not forget that it also exhibits the poorest divisibility.
A compromise must be made between the three aspects: symbol size, space complexity and higher divisibility. Babylonians were the first people to adopt Base-60 or the sexagesimal system, which was nothing less than genius. The system consists of fewer symbols than the symbols in Base-200 and exhibits less space complexity than the binary system. However, its most lucrative characteristic is that not only does it have the same number of factors as 200 (12), but unlike 200, it is trichotomous. This has rendered it the most convenient and therefore most ubiquitous system to keep time and, since being inherited by the Greeks, to study angles.

The dozenal system enjoys the same advantage. Systems like Base-12 or Base-60 are therefore wonderfully versatile number systems. Yes, 12 has fewer factors and higher space complexity than 60, but it is still trichotomous and the number of symbols in Base-12 is far less than in Base-60. There are only two more symbols than are found in the religiously followed Base-10 system, so learning the extra two symbols is not too high an obstacle to surmount. In this nature, Base-12 is truly profound: of all the versatile number systems, it is the easiest to learn.
Our use of the decimal system is purely based on habit. One is not even required to unlearn the entire decimal system; he or she must simply incorporate two additional symbols into the existing order. But… is it too late? The revolution will come at the maddening cost of rewriting a majority of math textbooks ever published. As of now, this is, no doubt, highly implausible.
Decimal’s Failed Stint
Neither the addition of two months to the original ten-month calendar, nor the notion of a 12-hour day and night was accepted in view of 12’s virtues, but the fortuitous effect is evident nonetheless. What was accepted in view of its virtues were the units of lengths and weights: 12 inches still make up a foot. However, everything was reshuffled when the decimal system was revived, and a majority of the units were metricized. In fact, for a brief period, even time was decimalized.

The French were enamored, or rather obsessed, with the Base-10 system, to the extent of inventing and following a calendar charting not seven, but ten-day weeks. The month was then not divided into four weeks but three decades. What’s worse is that they even decimalized the days! The length of a day was legally reduced from twelve hours to ten, whereby each hour comprised one hundred minutes, each of which comprised one hundred seconds. Each day was then 100,000 seconds long, as compared to the 86,400 seconds it is in a Babylonian 12-hour-60-minute-60-second day.
The citizens were required to work for not six, but nine marginally longer days every week! This was, as you would imagine, frightening. They followed this quirky, decimalized calendar for 12 years after the French Revolution, twelve long years after which its drawbacks could no longer be ignored and it was finally discarded for good.