Why Does Squinting At A Light Make A Plus Sign Shape?

When you squint, you are blocking at least 50% of incoming light; by tightening your eyelids, you are also bringing your eyelashes into your narrowed field of vision, which can create a vertical pattern as light is reflected off your eyelashes, rather than onto your cornea. This can cause the light to reflect onto the cornea in a uniquely geometric way, making it appear as though the light is shooting out beams of light at 90-degree angles.

When you squint your eyes, reducing the surface area being exposed to air, the tear film changes on your eye; essentially, the volume of fluid above your eye changes.

Think back to the last time you were walking home in the dark, looking up at strange street signs as you tried to get your bearings. Perhaps one of those signs was illuminated by a streetlight above, but as you squinted to read the text, the streetlight appeared to burst into a plus sign or a “star polygon” in your field of vision.

When you stop squinting, the perpendicular beams disappear, leaving you once again standing in the darkness. This type of visual phenomena is difficult to explain, considering that so many visual impairments may result in glare, star bursts or other light-related issues. However, even young people with perfectly health vision and no cataracts or impairments will also see this unusual phenomenon when they squint.

While it may seem like a banal phenomenon, it touches on elements of our visual processing system, the anatomy of the eye and the behavior of visual light. In other words, it’s a quirky phenomenon that is well worth exploring.

Recommended Video for you:

How Humans See

Before we can explain the visual phenomenon of a starburst shape when you squint at a light source, we should take a brief review of how humans are able to see at all!

To begin with, the light that we see is reflected off the objects in front of us and taken into the eye through the cornea. Our pupil control how much light is allowed to enter the eye, and is surrounded by the iris. Behind the cornea is the lens, which is what focuses the light entering the eye onto the retina, located at the back of the eye. Using tiny ciliary muscles to change its shape, the lens allows us to focus on things at varying distances and still discern what we’re looking at.

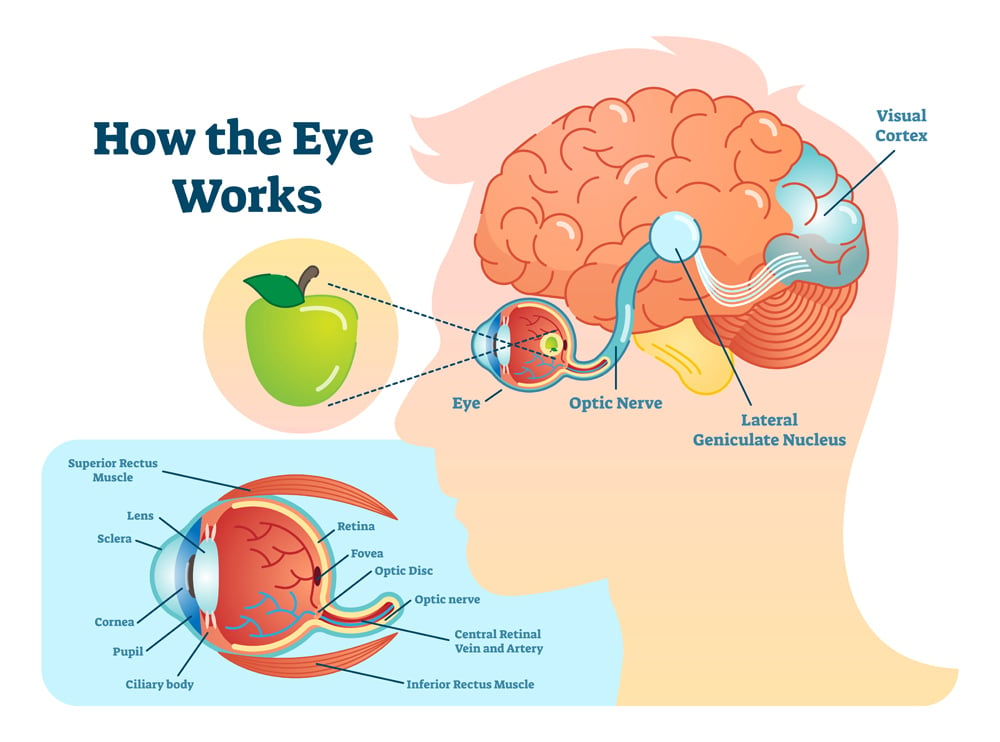
Once the light has been focused onto the retina, the energy in that focused light creates chemical signals on the retinae, which are transferred via the optic nerve to the brain, where the information can be processed into an image that we can understand and react to. Obviously, that is a rudimentary explanation of a very delicate, complex and nearly instantaneous process, but that should explain the basic elements that affect the larger question addressed in this article.

Don’t Look Into The Light!

Now, most humans beings know not to stare directly at the sun—unless you’re the American president during a solar eclipse, of course—because of how the eye works. Essentially, the lens of the eye can function like a magnifying glass, potentially focusing the intense light of the sun and burning a hole on the back of your retina, which can lead to permanent damage to your vision. Instinctively, perhaps for that very reason, when we stare directly at any bright source of light, we tend to squint.

This lessens the amount of light entering the eye, as it is blocked by the eyelid. This action diminishes the intensity of the light, and can also help us see things more clearly, by requiring the lens muscles to work less, thus producing a sharper image.

Now, when you look at a light source with open eyes, particularly against a dark background, you can often see a halo of light around it; if you are staring directly at a point source, you may actually be overstimulating your retinal cells, generating blotches of light (you can see them against a dark background, even after you turn away from the light source).

As you squint at the same light source, however, you will begin to see thicker, perpendicular rays beams or spikes of light around the light source, like a plus sign. There are a few theories out there that explain this particular phenomenon, two of which appear to be the most plausible. When you squint your eyes, reducing the surface area being exposed to air, the tear film changes on your eye; essentially, the volume of fluid above your eye changes. Incoming light behaves differently in these conditions as it interacts with the fluid and is refracted through the cornea.

Other Explanations For This Visual Phenomena

As mentioned, it can be difficult to separate the experience of this natural phenomenon with the experience of glare or halos, both of which may hint at underlying vision issues. While seeing plus signs may be a natural physical response of the eye, some other causes of distracting light phenomena may require medical attention, or may simply be a “trick of the light”.

Cataracts are a major contributor to such problems, as they obscure the path of light into the eye, thereby scattering instead of focusing the light. This can make images look blurry or make a light seem uncomfortably bright, giving it a halo or glare effect.

If you suffer from astigmatism, nearsightedness or farsightedness, the natural shape of your cornea or eyeball, respectively, may prevent light from being properly focused on your retina, leading to the development of glare, making it difficult to focus or see properly.

Finally, if you are squinting your eyes, you are already blocking at least 50% of incoming light; by tightening your eyelids, you are also bringing your eyelashes into your narrowed field of vision, which can create a vertical pattern as light is reflected off your eyelashes, rather than onto your cornea.

A Final Word

If you’re seeing spikes of light or glare every time a light source enters your field of vision, it is definitely time to see an eye doctor and get yourself checked out, but don’t freak out when a lone streetlight in the distance appears to be shooting out beams of light at 90-degree angles. This is simply due to a greater accumulation of fluid around the edge of your eyelid, which causes the light to reflect onto the cornea in a uniquely geometric way.