What Effect Does The Spin Of An Electron Have On Macro Levels?

Electron spin contributes to the Zeeman Effect, which is used to study magnetic fields in interstellar space and predict star formation.

When you hear the word electron, what comes to mind is probably an extremely small, negatively charged sphere, the electronic configuration of elements, and possibly the fact that electric current is due to the flow of electrons in a wire. However, being charged and in motion, they also have magnetic properties, which give rise to quite a few interesting phenomena at the quantum scale, that even have consequences at the interstellar scale.

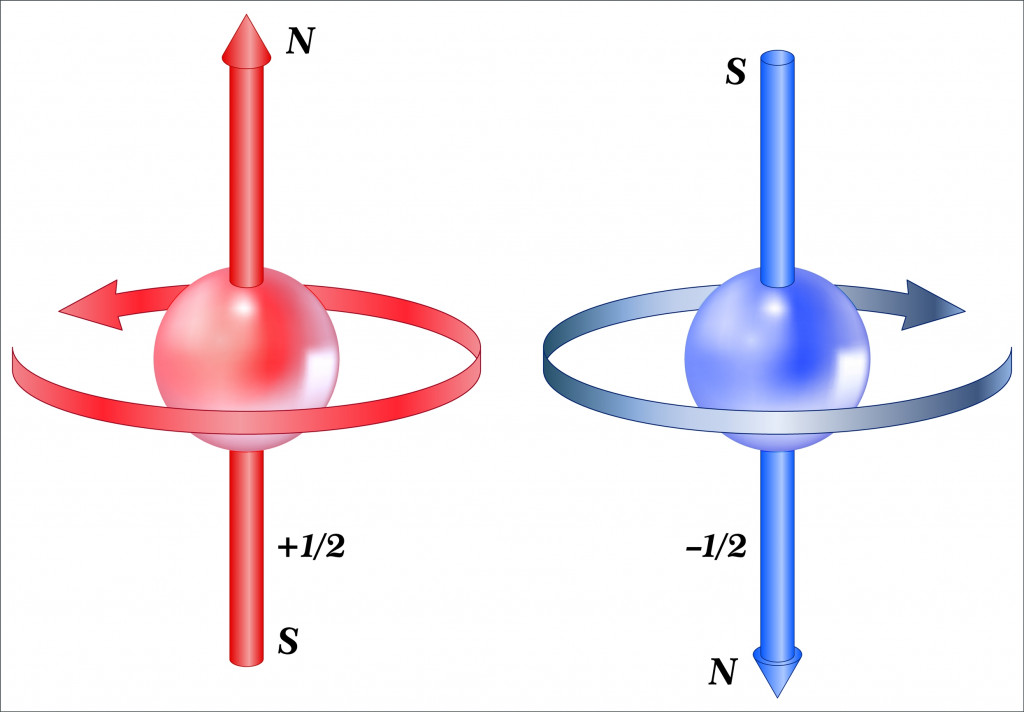
The intrinsic property of electrons that contributes to magnetism is called spin. To understand the effects of spin at the macro scale, it’s important to first understand what spin is.

Recommended Video for you:

Electron Spin: A Misnomer

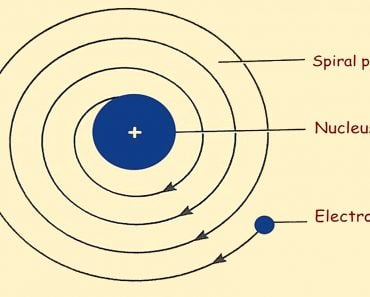
Bohr’s theory of the atom was an extension of the classical theory to the quantum world. In essence, electrons were assumed to be orbiting the nucleus, just as Earth orbits the sun. Thus, the entire mathematical framework of the sun-earth system (calculation of angular momentum, angular velocity, the energy of rotation and revolution, etc.) was extended to the electron-nucleus system.

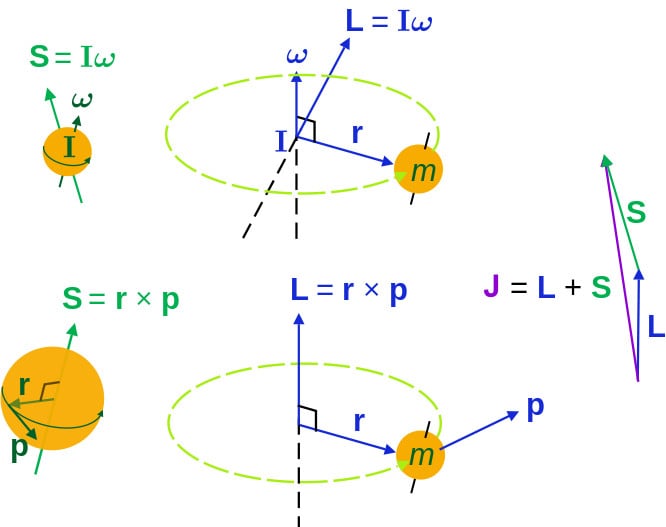
Since an electron behaves as a point charge with no spatial mass distribution, the spinning analogy of classical mechanics was discarded and only the orbital analogy (i.e., revolution about the nucleus) was retained. Thus, an electron was assumed to have orbital angular momentum and an associated orbital magnetic moment.

Later experiments showed that electrons have an intrinsic magnetic moment and an intrinsic angular momentum, which are independent of the orbital component.

This was christened spin angular momentum and spin magnetic moment because it made sense when thought about from the classical perspective. Electrons don’t spin because it would break the laws of special relativity. Spin is therefore a misnomer and must not be confused with the physical spinning of objects.

Effects Of Electron Spin: The Zeeman Effect

Consider a Hydrogen atom. Bohr assumed that there are only specific orbits that an electron can take. Those were called stationary states. A convenient way of representing these was by using the principal quantum number n, where n represented the orbit number. For example, n=1 was the lowest orbit (closest to the nucleus and the most stable), n=2 was the next allowed orbit with energy higher than n=1. Likewise, further orbits were designated as n=3, 4, 5, …, etc. The greater the value of n, the greater the electron’s energy.

The n^th orbit is given by:

, where

h = Planck’s Constant,

m = Mass of the electron,

v = Linear velocity of the orbital motion of the electron,

R = radius of the n^th orbit

Providing energy to the electrons promotes them into higher energy states (from n=1 to n=2, 3, 4, …, etc.). When the energetically excited electrons fall back to the ground state, they emit electromagnetic radiation with an energy equal to the energy difference of the two principal quantum states. These transitions can be viewed through a spectrometer, and the spectrum is called an emission spectrum.

When the emission spectrum of Hydrogen is analyzed in the presence of an external magnetic field, a strange phenomenon occurs. Bohr’s theory correctly predicted the splitting of lines into triplets for the n=3 to n=2 transition, only taking into account the orbital angular momentum. Yet when the spectrum of Sodium is analyzed, the lines corresponding to various transitions, such as n=3 to n=2 or n=4 to n=3 split into more than three lines, which was not predicted by Bohr’s theory.

It could only be explained by the existence of an intrinsic magnetic moment, called the spin magnetic moment. This spin magnetic moment interacts with the orbital magnetic moment to produce the multiple closely spaced lines.

Mathematically, orbital and spin magnetic moments are given by:

and  respectively, where,

= Spin Magnetic Moment and Orbital Magnetic Moment, respectively,

e = charge on electron

m = mass of the electron.

, = Orbital Angular Momentum and Spin Angular Momentum, respectively,

= Bohr Magneton,

= Lande’s spin g-factor ~ 2.002

When these two add up, the resultant magnetic moment is given by

This magnetic moment is responsible for the Zeeman Effect. The splitting of lines in the presence of an external magnetic field implies that a frequency change also occurs. The frequency shift is given by:

where

= unshifted frequency

g = Lande’s g-factor

B = Magnetic Field Intensity

= Bohr Magneton 

h = Planck’s Constant

From the above equation, B can be calculated if the frequency is known. This frequency is measured using a spectrometer.

Effects Of Spin At The Macro Scale

We’ve seen that spin magnetic moment interacts with the orbital magnetic moment and the external magnetic field, such that the energy levels split up. At the macro scale, this is used in astrophysics.

Studying Star Formation In Interstellar Space

Interstellar space is made up of various gases, such as H₂, CO, OH, HI, etc., the most abundant being Hydrogen gas. These gases, along with very fine dust particles, create a gas cloud. Since gravitation is an intrinsic property of mass, these gases cluster together to form large gas clouds, which increases the mass density in that region of space, resulting in greater gravitational force, which accumulates even more matter. Thus, a positive feedback loop is created where gravity compresses mass together, resulting in an increase in gravitational attraction due to the compressed mass.

Interstellar space also contains weak magnetic fields of the order ~ 3uG – 6uG. In equilibrium conditions, this magnetic field balances the gravitational attraction of gas clouds and prevents further mass accumulation. The ratio of magnetic flux to cloud mass is useful for studying star formation.

Theoretical Predictions

Assuming a spherical interstellar cloud mass, the equilibrium ratio of magnetic flux (amount of magnetic field present in that region) to cloud mass, called critical mass-to-flux ratio is given by:

where,

M = Mass of the gas cloud

= Magnetic flux 

G = Universal Gravitational Constant ~ 6.674 10^-11 m³/kg/s²

This is the theoretical critical ratio based on calculations where gravitational pull is balanced by magnetic forces.

Spectral Observations

The emission spectrum from this region of space is analyzed and the actual strength of the magnetic field B is calculated using the following equation:

, from which flux, is calculated.

The mass of the gas cloud is observed (this process is beyond the scope of this article), and the observed ()_o ratio is calculated.

Case I: If , then the cloud mass is supercritical and the magnetic field is unable to stop the gravitational collapse of mass onto itself, resulting in potential star formation.

Case II: If , then the magnetic field alone is enough to stop the gas clouds from gravitational collapse.

A Final Word

Electrons have two magnetic moments associated with them, an orbital magnetic moment and a spin magnetic moment. The interaction of these moments gives rise to the splitting of energy levels in the presence of an external magnetic field, a phenomenon called the Zeeman Effect.

Interstellar space contains weak magnetic fields too. When a region of interest is observed, the emission spectrum also contains fine lines, corresponding to the split energy levels. This is then used to calculate the magnetic field in a given region of space.

In this way, a quantum phenomenon can be used to observe macro-scale effects!