How Many Holes Does A Drinking Straw Have?

Math says a drinking straw has a single hole.

There are certain questions that seem to summon answers with very opinionated supporters on each side. Whether you’re chatting over drinks or debating in Reddit forums, these questions seem to bring out the debating fire in everyone.

Which came first, the chicken or the egg? Are zebras black or white? How many holes does a drinking straw have?

The answer to that last question is simpler to think through than the others, but we need to turn to mathematics for clarity.

Recommended Video for you:

The Drinking Straw Debate

So… how many holes does a straw have? The question might seem confusing to some, while the answer might seem obvious to others. Even if an answer seems obvious, we need to get there scientifically.

Are there one or two holes in a straw? There are those who passionately defend both answers. Some even say that a straw has an infinite number of holes. Others have gone so far as to claim that a straw has zero holes.

The zero hole group might argue that a straw is simply a bent plane. Since the plane doesn’t have any holes, and you can bring the edges together to make a straw, the straw has no holes. However, by bringing the edges together, you are making a hole, so that argument doesn’t hold up too well, unless you’re questioning the very existence of holes themselves.

Assuming you believe in holes, the other variations in counting holes can mostly be traced to the basics of the argument—how one defines a hole.

What Is A Hole?

Defining a hole is a “whole” other heated debate in itself. There are questions of whether a hole is a presence or an absence, or whether they are things that can be physically defined at all. However, let’s not get too deep into that today.

When we talk about holes, we could be talking about something that could be filled or something through which something else could pass. We have blind holes—a hole in the ground or the hole in a vase—and through holes. Topologically, when we talk about holes, we’re only considering the second kind.

You could say that a glass has one hole in it, which we fill with coffee or any other liquid. However, if we flatten the glass down, it would ultimately become a plate. We can all agree that an undamaged plate doesn’t have a hole. Thus, if a glass has a hole, we would have to define some point in the flattening process when the hole stops existing.

The topological definition of a hole is that it’s a structure that prevents an object from being shrunk to a point.

If we took a circle and shrunk it down, it would never become a point. The space inside the boundary prevents it from doing so. Hence, a circle has one hole.

A donut, similarly, would have one hole. A hollow torus, which is something like a hollow donut, will have two holes. Both the hollow space in the middle of the torus and the space inside the torus prevent it from ever being shrunk to a single point.

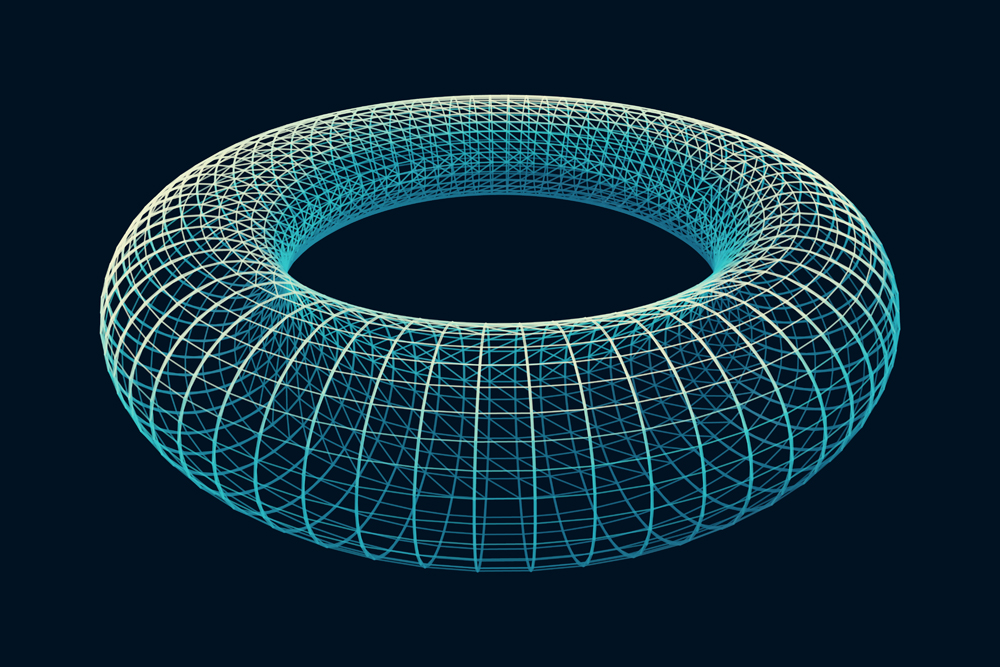
Let’s look at the “number of holes” debate, while staying inside this topological definition.

Counting Holes

We’ve established that a circle has one hole. From here, we can see the one-hole camp and the two-hole camp.

Does A Straw Have Two Holes?

This is the argument claiming that a drinking straw has two holes. A straw is a cylinder, in which two circles at each end can be traced. Two openings = two circles = two holes. A hole through which stuff goes in, and another through which stuff comes out.

Going by the topological definition of a hole, this argument is invalid, as it is treating an opening as a hole. The number of openings does not define the number of holes.

We’ve established that the hollow space inside the torus is a hole, even though it has no openings. The hole is the space enclosed in the boundary, not the boundary itself.

We’ve also said that topologically, a glass or a cup doesn’t have a hole. In order to go with the thinking that a drinking straw has two holes, we would need to negate this. If a straw has two holes, then a glass has one.

Does A Straw Have Just One Hole?

Topologically, a straw is the product of a unit circle and an interval. The interval is the length of the straw. The circle has one hole, and the interval has no holes. Therefore, a straw has a single hole.

It’s not two circles at each end of the straw, but rather, the same circle!

To envision this, imagine squishing down the straw. Its length will shrink until, at some point, it looks more like a ring or a washer. At this point, it should be clear that it only has one hole. If it had more than one, there would have to be some indescribable point where the other hole disappears, which doesn’t seem probable.

Let’s look at it a different way. According to mathematician Bernhard Riemann, the number of holes equals the number of times an object can be cut without resulting in two separate pieces. For a torus, you can cut it twice with it still remaining a single piece. For a circle or a ring, you can make just one cut along the boundary without causing separation.

Similarly, for a straw, you can make a single cut along its length. Any further cuts would separate it. Hence, a straw has a single hole.

Building on these ideas, topologists now use Betti numbers, introduced by Henri Poincaré, to define the number of holes. All answers double down on one result—a straw has exactly one hole.

A Settled Debate

Mathematics tells us that a straw has only one hole. The supporters of the two holes theory may not be so easily appeased, as we can see in those heated debates on Reddit. It seems as if there is enough proof to disregard them, so the debate is settled!