How Does Game Theory Deal With Irrational Actors?

The formal basis of game theory is rationality. Since real-life players are not rational, a few methods have been created to deal with such irrationality.

In 500 BC, a book called “The Art of War” was written by Sun Tzu, a Chinese military strategist. If you have read it, you already know how the treatise remains relevant, even in today’s world. In his book, Sun Tzu writes about how to win a war. He emphasizes strategy-making, which he writes is more important than just upgrading weapons. Know thy enemy is the cardinal principle. It seems that Sun Tzu understood game theory long before it could be penned down.

Game theory is the formal study of decision-making that uses applied mathematics to analyze the choices of several players in a situation. The decision of the players is often interdependent; thus, each player curates their strategy based upon the possible strategies of other players.

Any such situation involving decision-making is called a game. It’s not necessary that a game be some kind of playtime activity like carom or pool. The applications of game theory are much broader than that. It can just as easily be applied to companies formulating their marketing techniques or to a group of friends deciding what to eat in a restaurant.

Sun Tzu unknowingly linked game theory to war. Though he did not come up with any mathematical analyses, he knew that to win a war, one must be aware of a competitor’s strengths and weaknesses.

Recommended Video for you:

The Development Of Game Theory

Numerous theorists have come up with game theory-like analyses, like Antoine Cournot’s study of duopoly in 1838 and Emile Borel’s study of games in 1921. However, the first formal development in this field was the 1944 publication “Theory of Games and Economic Behavior.”  The book was authored by mathematician John von Neumann and economist Oskar Morgenstern. Neumann had earlier (in 1928) published a paper that was similarly titled ‘On the Theory of Games of Strategy.’

Both Neumann and Morgenstern came up with a rationale that the mathematics used in day-to-day life cannot be applied to solve problems in economics. According to them, the field of economics involves decision-making based on external circumstances. Thereby, they came up with game theory, which could prove to be more efficient.

Nash Equilibrium

In 1950, John Nash, an American mathematician, came up with his own decision-making model famously known as Nash equilibrium. In a game, Nash equilibrium is a condition in which each player only has a specific set of strategies to choose from. Since every player is rational and wants the best possible outcome, no one would dare to change their strategy unilaterally. For example, if all the countries possess similar strengths and weaknesses; none would wage a war against each other, as it would not be in their best interest. In case a country decides to do so, others might form a coalition against it.

Since John Nash, there have been many scholars and Nobel laureates, like Thomas Schelling and Robert Aumann, who have contributed to the further development of game theory.

Prisoner’s Dilemma

A classic example of game theory is the case of prisoner’s dilemma. It pertains to an imaginary setting in which two prisoners have been accused of a crime. They are faced with a situation in which, if neither of them confesses, they will have to serve 2 years in prison. If both of them confess, both will have to serve 5 years in prison. However, if only one of them confesses, he or she will be acquitted, whereas the other one will have to suffer 10 years imprisonment.

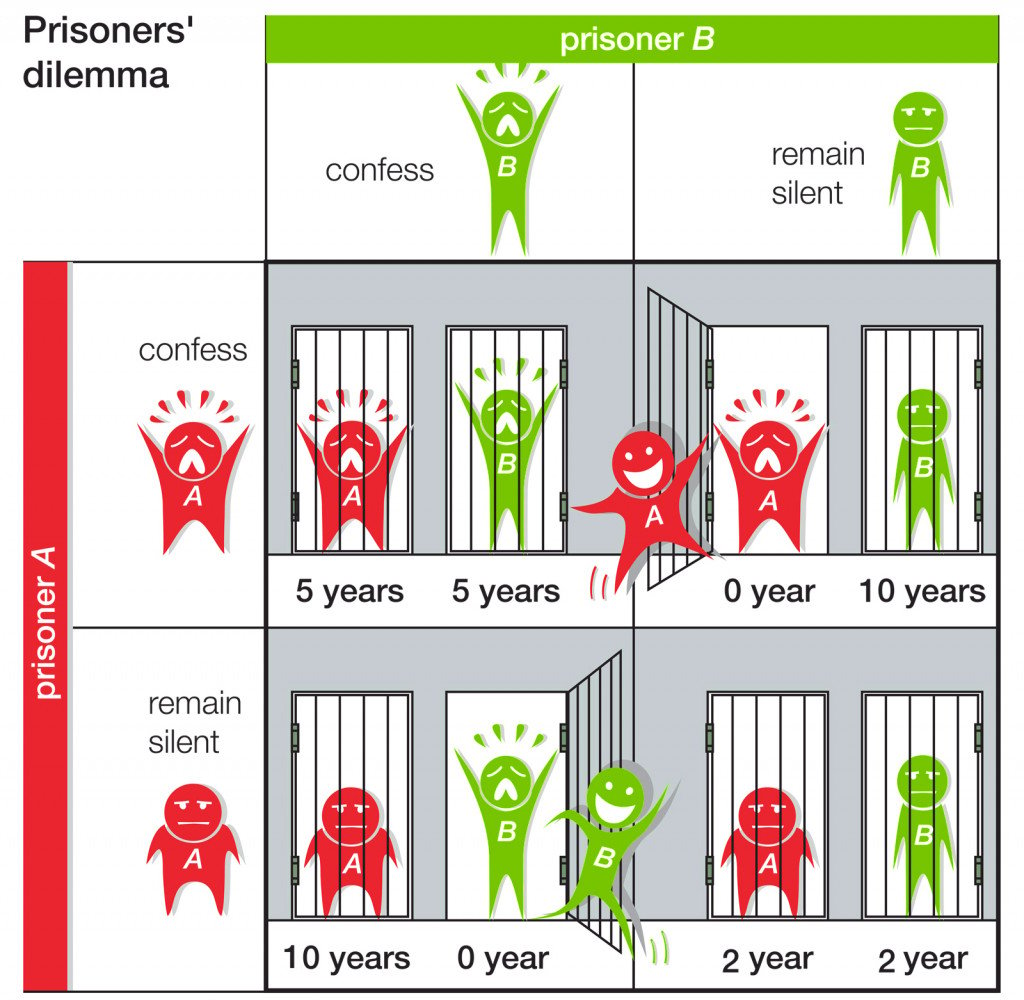
Since neither of them knows what the other might say, it is in the best interest of both to confess to the crime. This is because, in case one of them confesses, it will become the worst-case scenario for the other. Furthermore, the condition where neither confesses is quite bleak, due to the lack of mutual trust.

The prisoner’s dilemma can arise in any kind of situation. For example, if all people cooperate to keep their surroundings clean, everyone will experience lesser pollution. However, this condition is not an equilibrium condition, as there will always be some who will prefer not to work hard to clean, thus putting a burden on others. Therefore, the most suitable condition turns out to be the one where no one cleans, causing a rise in environmental pollution. This can also be stated as one of the reasons why climate talks fail.

Assumptions In Game Theory

Game theory is a mathematical model and thus works on certain established principles and assumptions. The foundation on which game theory functions is rationality. A rational player is one who is able to choose the outcome that has the maximum payoff. Rationality is based on two ideas—transitivity and completeness.

Completeness signifies that a player is smart enough to rank their preferences in order. For example, if a person is confused about which fruit to buy, not because they like all the fruits equally, but because they are unaware of their likes and dislikes, such a player is not considered rational.

Transitivity means that a player is consistent. This means that if a person likes guava the most, they will always buy guava over other fruits.

Game theory also assumes that all players have common knowledge. This means that all are aware of the rules of the game and any changes that might occur in rules. For instance, when two players are engrossed in chess, they must abide by certain rules. No player can make random moves just to win the game. It also signifies that all players are aware that everyone knows the same things and that all players are rational.

Game Theory And Irrational Actors

Even though rationality is the crux of game theory, it is quite a debatable issue. According to a number of scholars, the assumption of rationality in game theory is merely rhetoric. In a number of real-life experiments, it has been found that people often do not comply with all the rules of rationality. Players might be unaware of their choices (lacking completeness) and might also not be consistent in their choices (lacking transitivity).

In fact, when the backward induction method (a method by which results are used to analyze the beginning of the game) is used, it is found that players cooperate only to a certain level of the game. Thereby, without cooperation, some players might end up with indiscriminately high payoffs, which are not possible if equilibrium is to be maintained.

When this happens, other players end up with payoffs that are much less than the maximum payoff. This shows the failure of common knowledge, as to achieve a very high payoff, some players might either be hiding information or tweaking rules for their own benefit.

Dealing With Irrational Actors

One of the solutions to deal with irrationality is the use of bounded complexity. In this, all the players are provided with a limited set of solutions. Such a case makes decision-making an easier process and helps in dealing with irrationality.

For example, if all the soldiers fighting a war start thinking rationally and try to maximize their benefits, they will not fight, but instead run away from the battlefield. This is because, whether they win or lose, there is a probability of losing their life. Considering the most favorable outcome, a soldier might desire to live, instead of dying, and thus run away.

Spanish conqueror Cortez realized this hundreds of years ago. before he decided to attack Mexico with his small army. Faced with the Aztecs, he feared that his troops might try to escape. Thus, as soon as his troops landed, he burned all his ships, eliminating the option for escape.

Conclusion

Although game theory does come with its own flaws, it remains one of the greatest contributions to the field of decision-making. Its wider applicability makes it even more favorable. The mathematical model is especially useful in making sure that no one reaps extra benefits. Game theory has turned out to be an evolutionary science, so over time, we can expect even more modifications and corrections. Game theory might be able attain perfection in the future, but only time will tell!