Table of Contents (click to expand)
Angular momentum is the measure of how much motion a mass has when moving in circular orbits or rotating about itself.
While enjoying a delightful ride on a carousel, or riding your motorcycle to work, or when a ballerina spins gracefully in circles, or when the Earth revolves around the moon, what we are experiencing is angular momentum in action.

Angular momentum is one of the most important physical quantities and qualities of nature. In fact, the conservation of angular momentum is the reason for our very existence.
However, before we start talking about angular momentum, let’s have a quick recap of momentum itself.
Recommended Video for you:
What Is Momentum?
In sports, we say that when a team performs really well at an event, it will take a tremendous amount of effort from other teams in the future to stop its winning streak.

In other words, you could say that momentum makes it difficult to change the state that one is existing in at the moment.
That’s exactly how momentum works in physics! Momentum is the quantity of motion that an object possesses. Think of it as an invisible quantity that things attain once they move.
Momentum tells you how much a certain amount of mass is moving. Just as a winning team needs a stronger opponent to stop their consecutive victories in sports, once an object has gained momentum, you need to apply an external force on the object to change its state, i.e., make it stop.

So momentum depends on how much mass there is and how fast that mass is moving, giving the equation:

P in this equation stands for momentum (since the letter m is already used for mass, scientists use P for momentum from the Latin word Pellere meaning “to push something forcefully”), while v stands for velocity.
The little arrows on top of P and v signify that these are vector quantities, meaning that they have direction as well as magnitude. Thus, when we talk about the momentum of something, we mention how much of it is present and in what direction it is going.

What Is Angular Momentum?
When we introduced momentum, we talked about the motion of the objects in a straight line, but what if the object is just rotating or revolving?
Well, when an object is moving in a circular path, the angular momentum replaces the normal momentum.
Imagine a circle with a small dot at the center. An object moves over the perimeter of this circle. We have already seen that when an object sets into motion, it gains momentum, so now that the object is moving in a circle, it will gain angular momentum.
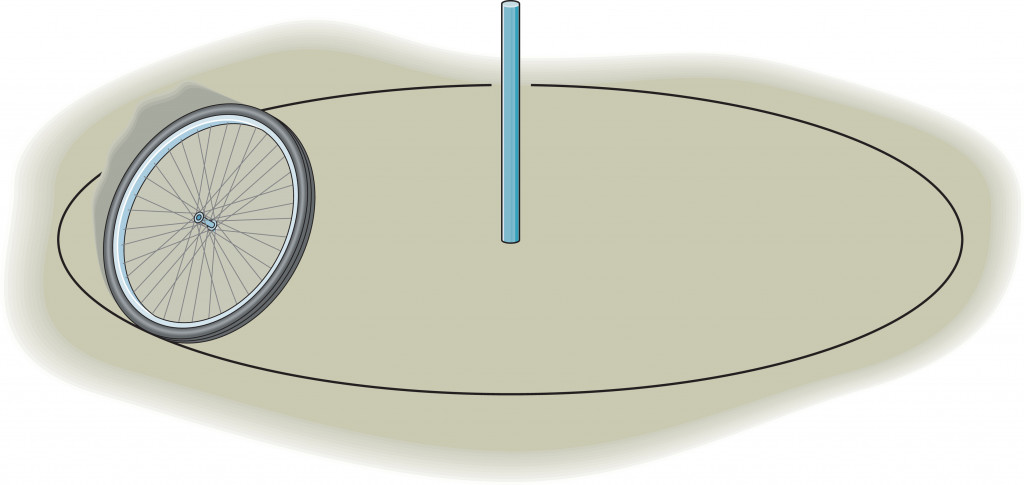
Angular momentum is very similar to momentum. Whereas momentum tells us how much motion a thing has when it is moving in a straight line, angular momentum tells us how much motion an object has when it’s following a circular path.
It is called angular momentum because the angle at which the object is moving from a reference line is constantly changing.
The equation for angular momentum is also very similar to that of momentum.

The product of mass, the velocity that the object has in the tangential direction to the Perimeter of the circle, and the radius of the circle give angular momentum.
Another way to mathematically visualize angular momentum is using the moment of inertia, which acts as mass for objects moving in circular orbits, and angular velocity, which, as the name suggests, acts as velocity for objects in either circular or rotational motion.
We get an equation very similar to that of momentum when we use these two quantities as:
 Where I is the moment of inertia and ω is the angular velocity.
Where I is the moment of inertia and ω is the angular velocity.
Conservation Of Angular Momentum
The most important quality of angular momentum and the reason it is so important in our lives is that it is conserved. Conservation of angular momentum means that the total angular momentum within a system stays constant, unless there is some outside torque (which is the force that makes objects spin) that causes a change. In other words, the angular momentum stays the same as long as one does not disturb it.
If there are a certain number of objects in a system (i.e., there are some objects moving around nearby), their total angular momentum would always remain constant.
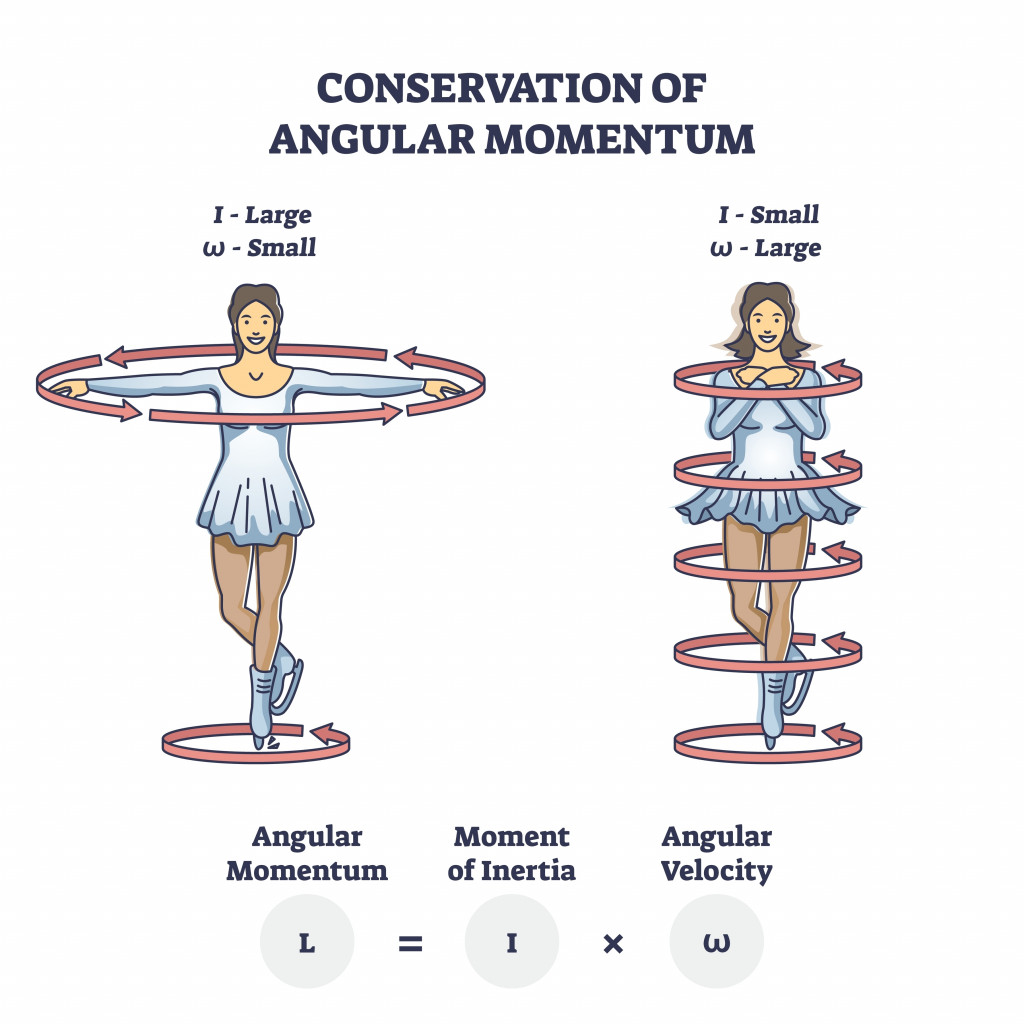
A ballerina can spin faster when she draws her arms in because when the radius of the spinning decreases, the speed of the spinning increases in order to keep the angular momentum constant (or in other words, to make sure that the angular momentum is conserved).
It is an astounding thought. It is as if nature has its own will and ensures that angular momentum is conserved no matter what by making adjustments to the motion of the objects.
Conclusion

Angular momentum is just a different form of momentum, experienced when an object is moving in circles. It can be thought of as the quantity that tells how much motion an object is taking while moving in a circular path.