What Is A Capacitor?

A capacitor is an electrical component that stores charge in an electric field. The capacitance of a capacitor is the amount of charge that can be stored per unit voltage. The energy stored in a capacitor is proportional to the capacitance and the voltage.

When it comes to electronics, the significant components that serve as the pillars in an electric circuit are resistors, inductors, and capacitors. The primary role of a capacitor is to store a certain amount of electric charge in place. The funny thing about capacitors is that you can actually see them floating around in the sky! Yes, that’s right… nature’s form of capacitors are clouds. They store energy just like a more traditional capacitor and discharge it during storms when they have collected enough of an electric charge. That being said, let’s turn our attention back to small man-made capacitors and try to understand precisely how they work.

Recommended Video for you:

Theory Of Operation

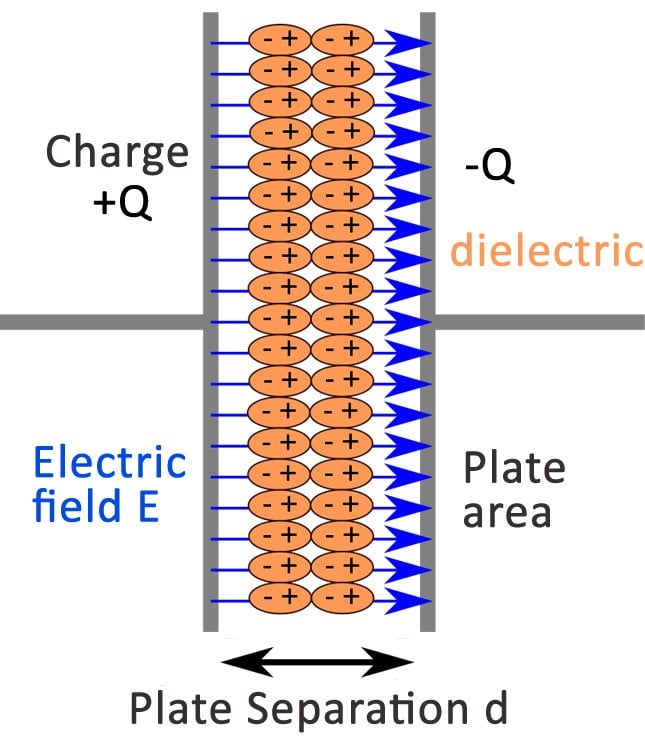
A capacitor is a device that consists of two conductors separated by a non-conducting region. The technical term for this non-conducting region is known as the dielectric. The dielectric can be any non-conducting element, including a vacuum, air, paper, plastic, ceramic or even a semiconductor.  Now let’s get into how the charge inside the capacitor is developed.

Lets first try to understand a fundamental law known as Coulomb’s Law, which states that like charges repel and opposite charges attract, with a force that is proportional to the product of the electric charges and inversely proportional to the square of the distance between them. Now, using this law, we can explain that the charges that build up on one plate of the capacitor exert a force on the charges of another plate of the conductor. The like charges will attract one another, while the opposite charges will repel one another. This causes the surface of the conductors to develop and hold equal and opposite charges. The dielectric present between the two conductors develops an electric field passing through it.

If one were to try and visualize how a capacitor would work in a less rigorous way, we can always take up a hydraulic analogy to help make the visualization easier. Let’s imagine that a rubber membrane is present in a pipe with flowing water  in it. Now the membrane, in this case, is the analogous equivalent to a capacitor. Water cannot move through the membrane, but some can if the membrane is stretched to its maximum extent. This analogy clarifies a few things for us:

• The current alters the charge of the capacitor, just as the water stretches the membrane. This touches upon the fact that one plate of the capacitor has more charge and the other plate is observed to have a decrease in charge due to Coulombs Law. This is again similar to the rubber membrane, as the amount of water on one side increases comparatively to the amount of water on the other side.
• The more a capacitor is charged, the larger the voltage drop that will be experienced by the capacitor. This is analogous to the fact that the rubber membrane pushes back on the water in proportion to how far it is stretched.
• A funny phenomenon occurs, namely that charge can still flow through the capacitor, even if no electrons physically cross to the other side. This is analogous to the water flowing through the pipe. Even though no water molecules can flow through the membrane, the flow cannot continue in the same direction forever. The rubber membrane will have to break and allow the water to pass by at some threshold point, which is analogous to the dielectric breakdown in a capacitor.

Capacitance, Voltage, Power And Energy

In quantitative terms, the capacitance is the charge per unit voltage that can be stored by an element. The capacitance of a capacitor can be imagined as the volume of a water bottle. The larger the bottle, the more water it can store; similarly, the larger the capacitor, the greater will be its capacitance value. The formula for the capacitance of a capacitor is:

C=Q/V

The unit of capacitance is Farad (F). The capacitance is said to be one Farad if one coulomb of charge can be stored with one vault across the two ends of a capacitor plate. In the above equation, Q signifies the amount of charge that is stored and V is the voltage or the potential difference the capacitor experiences.

Now, let’s try to understand how the energy is stored in a capacitor, which requires a bit of mathematical rigor. The current flowing through any device can be calculated as the amount of charge flowing through a unit of time.

I=dQ/dt

By rearranging the value of the capacitance of a capacitor, which is as follows:

C*dV=dQ

Now, by plugging in the rearranged formula back into the current formula (I=dQ/dt), we obtain the following formula:

I=C*dV/dt

By cross-multiplying and taking definite integrals on both sides by taking the limits before it was charged to the point where it is completely charged, we get the following formula:

The above formula gives the voltage and current of the capacitor after a due charging period T. The power of a capacitor can be obtained by using the standard electrical power formula, which is as follows:

P=VI

In the above equation, P stands for the power absorbed by the capacitor. V and I stand for the voltage and current of the capacitor, respectively. Now, by plugging in the current formula (I=C*dV/dt) of a capacitor, we get the following formula:

P=V*C*(dV/dt)

The energy consumed by a consumer can be obtained by taking the integral of the above power, and a small one-line calculation can be performed in order to arrive at an elegant solution:

With this, we can conclude that the capacitor is truly a powerhouse for storing electricity as electric potential. With this in mind, during the next thunderstorm, you can turn to your frightened friends and inform them that the lightning is actually being created by the biggest capacitors on the planet!